De
investigación
Propuesto
por Juan Bosco Romero Márquez, profesor colaborador
de la Universidad de Valladolid.
Problema 344.- Caracterizar y construir el triángulo ABC,
que es rectángulo en A, de hipotenusa a=BC, y de catetos b=AC y c=AB, de
tal forma que, BD=DE=EC, donde D es un punto tomado sobre AC, E es un
punto tomado sobre BC, tal que el ángulo ABD=ACB, y el ángulo BDE es rectángulo
en D.
Calculad también, los radios de los círculos inscrito y circunscrito a
cada uno de los triángulos ABD, BDE, DEC.
Romero,
J.B (2006): Comunicación personal.
Solución parcial de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.-
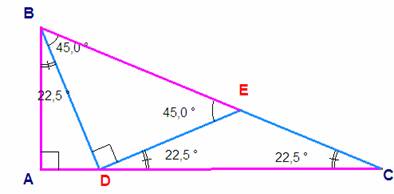
Según las
condiciones exigidas, el triángulo rectángulo BDE es isósceles, lo que nos lleva a que los ángulos iguales del
triángulo isósceles DEC tengan
amplitud 22º
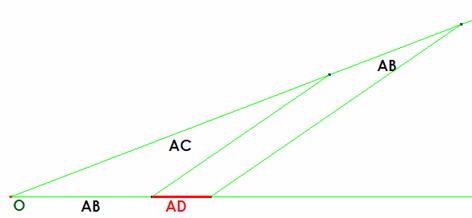
La relación de semejanza ![]() sirve para calcular AD
a partir de AB y AC, como muestra la figura de abajo y
con ello fijar la posición del otro punto E.
sirve para calcular AD
a partir de AB y AC, como muestra la figura de abajo y
con ello fijar la posición del otro punto E.