Aplicando el teorema
de la bisectriz al triángulo ABC tenemos que |
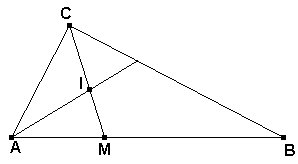
345. Razón de los segmentos que el incentro determina sobre la bisectriz. El segmento de bisectriz que va del incentro al vértice es a la suma de los lados del ángulo como el otro segmento al tercer lado. IC/(a+b) = IM/c Campo, S. (2005) Métodos sintéticos de la geometría. Edición de autor. Salamanca. (p.15) |
Solución de Francisco Javier García Capitán
Aplicando el teorema
de la bisectriz al triángulo ABC tenemos que
AM / CA = MC / CB.
Si llamamos k a esta razón tendremos
c = AB = AM + MB = k (CA +CB) = k (a+b), de donde k = c/(a+b).
Entonces es AM = k CA = bc/(a+b).
Aplicando ahora el teorema de la bisectriz al triángulo AMC, tenemos
MI/IC = AM/AC = (bc/(a+b))/b = c/(a+b).