De
investigación
Problema 345.-
Razón de los segmentos que el incentro determina sobre la bisectriz.
El segmento de bisectriz que va del incentro
al vértice es a la suma de los lados del ángulo como el otro segmento al tercer
lado.
IC/(a+b) = IM/c
Campo,
S. (2005) Métodos sintéticos de la geometría. Edición de autor. Salamanca.
(p.15)
“La
geometría es la gran olvidada de los planes de estudios actuales, y sin
embargo, citando a E. T. Bell:
La
geometría encierra un tesoro riquísimo de cosas interesantes y medio olvidadas, en mayor número que cualquiera otra sección de
las matemáticas que una generación siempre con prisas no tiene tiempo de
disfrutar.
E.T. Bell Historia de las Matemáticas. Fondo de Cultura
Económica. México.
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.-
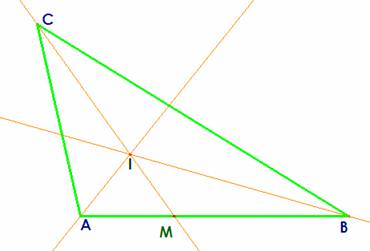
Los triángulos IBM e IBC tienen igual el ángulo en B, por ello la razón de sus áreas es la de los productos de los lados correspondientes, o sea,
pues
por el teorema de la bisectriz BM = 
.
Estos
triángulos tienen dos ángulos que son suplementarios: los de vértice en el incentro, por ello
. O bien
como se pretendía demostrar.