Problema:

En un triángulo ABC las cevianas AD, AE forman los triángulos ABD, ADE, AEC (no solapados) cuyos incirculos son iguales. Probar que: AD/AE=BE/DC.

Solución de Juan Carlos Salazar : Ver figura

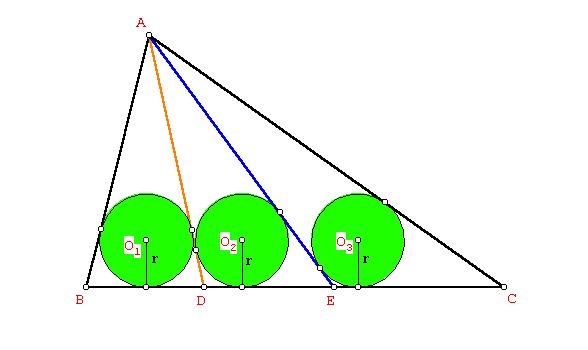
Denotamos:

s _ABE =semiperímetro ABE, s _ADC= semiperímetro ADC, r _ABE = inradio de ABE, r’_ABE = exradio de ABE opuesto al vértice A, r _ADC = inradio de ADC, r’_ADC= exradio de ADC opuesto al vértice A.

Conocemos:

AD = (s _ABE. (s _ABE - BE))^1/2= [ABE]/(r _ABE. r’ _ABE)^1/2

AE = (s _ADC. (s _ADC - DC))^1/2= [ABE]/(r _ADC. r’ _ADC)^1/2

Luego:

AD/AE = {[ABE]. (r _ADC. r’_ADC)^1/2}/{[ADC]. (r _ABE. r’_ABE)^1/2}

Como: r _ABE = r _ADC y también r’_ABE = r’_ADC

Entonces:

AD/AE=BE/DC