De
investigación
Propuesto
por de Juan Carlos Salazar, profesor de Geometría del Equipo Olímpico de
Venezuela.(Puerto Ordaz ).
Problema 346.- En un triángulo ABC las cevianas AD, AE
forman los triángulos ABD, ADE, AEC (no solapados) cuyos incirculos son
iguales.
Probar que: AD/AE=BE/DC.
Salazar,
J.C. (2006): Comunicación personal.
Solución.-
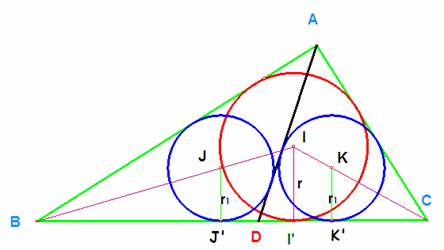
Comencemos por
un caso más sencillo. Vamos a suponer que se nos pide únicamente trazar una
ceviana AD de forma que los
incírculos de los triángulos parciales obtenidos sean iguales. Sean p el semiperímetro de ABC, d =AD y a = BC.
Para los triángulos de igual altura e incírculo ABD y ADC, se tiene
(1)
donde a’, a”, p’ y p” son las bases y semiperímetros respectivos.
Para las áreas [ABC]= [ABD] + [ADC], o bien pr = (p+d)r1. Despejando
(2)
Los incentros junto con los puntos de contacto con la base y los vértices B y C forman triángulos rectángulos. Son semejantes BJ’J y BI’I de una parte y CK’K y CI’I de otra.
Por tanto
=
(3)
siendo BI’= p — b, BJ’=p’— d; CI’ =p — c, CK’=p”— d.
De la igualdad entre la segunda y la última razón de (3) despejamos
(4)
De (2) y (4) eliminando los radios obtenemos
d2 =p(p-a) (5)
que
permite calcular d como media
proporcional entre dos segmentos. Un arco centrado en A con radio d corta a
lado BC en dos puntos D, D’.
La igualdad de
la primera razón con la última en (3) expresa el valor del segmento BJ’ =
que sirve para fijar el punto J’ y con él D y el
triángulo cuyo incentro es J.
Vamos a calcular ahora el radio r del círculo inscrito en el triángulo mayor ABC.
De (2)
obtenemos r =(1+d/p)r1. De (1)
y (5) 
, 
y finalmente
(6)
Expresión que sólo depende de la altura y el radio del incírculo. De ello se deduce que los triángulos del problema, ABE y ADC, tienen incírculos iguales, y al ser esto así, la razón entre sus perímetros es igual a la razón entre las bases respectivas (tomo e=AE)
o bien 
(7)
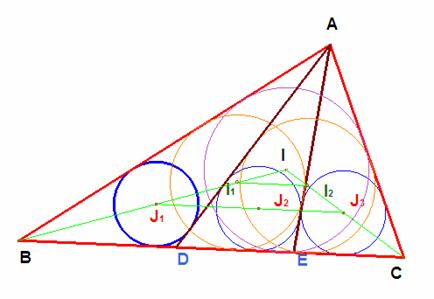
De (5) para el triángulo ABE tenemos d2 = ½ (c + e + BE)· ½ (c + e — BE), o bien
(c + e)2 = 4 d2 + BE2.
El mismo cálculo para ADC da
(d + b)2 = 4 e2 + DC2.
Sustituyendo en (7) después de elevarla al cuadrado resulta
=
Y simplificando
que es lo que se pretendía demostrar.
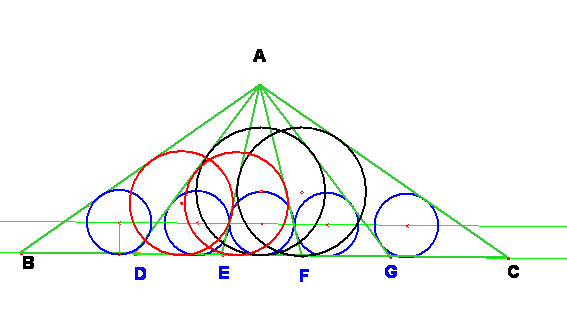
Reflexión final.-
En la última figura hemos puesto cinco triángulos yuxtapuestos de igual inradio e igual altura desde A.
Se puede generalizar el proceso de yuxtaponer triángulos de forma muy sencilla: se traza la bisectriz del ángulo AEF, ésta encuentra a la paralela a la base que pasa por los incentros en el incentro de un nuevo triángulo. Se une con A y ya tenemos otra bisectriz del nuevo triángulo. La recta simétrica de AE nos da el lado que falta.
Así añadimos el triángulo AEF. Y podemos seguir añadiendo los que queramos.
A raíz de esto nos planteamos si este proceso es finito o no. Los ángulos en los vértices que suceden al D van creciendo, el proceso finaliza si llegamos a sumar dos rectos, pero ¿eso sucede alguna vez? ¿Para qué triángulo inicial ocurre esto? ¿Es cíclico este proceso, se llega en algún momento a repetir uno de estos triángulos?
De otra parte hemos comprobado (=cabri nos ha mostrado) que las circunferencias inscritas en el triángulo formado por tres triangulitos adosados también tienen el mismo radio. ¿Sucede siempre esto? Ya hemos visto que con dos triángulos es cierto, lo cual parece asegurarnos que también lo es para cuatro, ocho,… y en general 2n triángulos. ¿Y para otras agrupaciones de triángulos?
Preguntas que tal vez el profesor Juan Carlos Salazar, que propuso el problema, sea capaz de responder.