 Si son conocidos
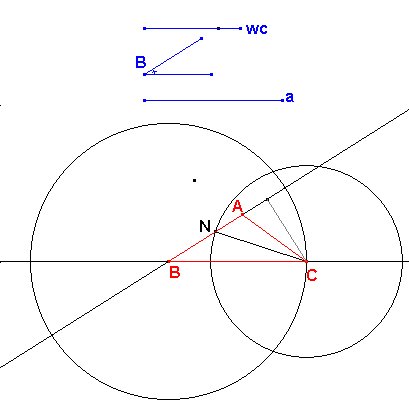
a, B y wc, podemos construir el triángulo fácilmente
Si son conocidos
a, B y wc, podemos construir el triángulo fácilmente
|
Construir un triángulo conocidos la longitud del lado a, el ángulo B y la medida de la longitud de una de las bisectrices interiores wa ó wc. |
|
Propuesto por Francisco Alcubilla.
|
Solución de Francisco Javier García Capitán
 Si son conocidos
a, B y wc, podemos construir el triángulo fácilmente
Si son conocidos
a, B y wc, podemos construir el triángulo fácilmente
Para que el problema tenga solución debe ser wc < a. Además, wc debe ser mayor o igual que la distancia de C a la segunda recta.
En este caso no vemos una solución tan rápida como en el anterior y recurrimos a la geometría analítica. Para ello nos preparamos con unas cuantas funciones de Mathematica que nos simplifiquen los cálculos:
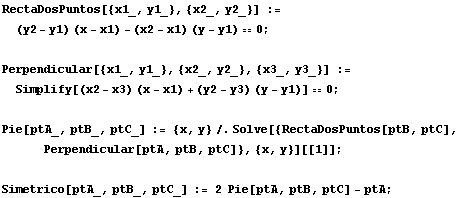
 Ahora consideramos
al punto B como origen de coordenadas y a la recta BC como eje
x. La recta BA tendrá ecuación y = mx
siendo m la tangente del ángulo B.
Ahora consideramos
al punto B como origen de coordenadas y a la recta BC como eje
x. La recta BA tendrá ecuación y = mx
siendo m la tangente del ángulo B.
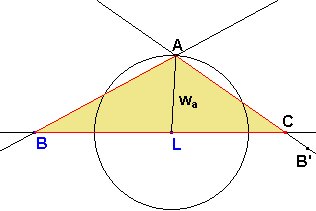
El pie L de la bisectriz del ángulo A sobre la recta BC será un punto a determinar, con coordenadas (t, 0). El vértice A estará localizado sobre la recta y = mx, a una distancia wa de L.
Para hallar el tercer vértice C hallamos el punto simétrico B' de B respecto AL y entonces el punto C será la intersección de AB' y BL.
La cuestión aquí es determinar dónde hay que considerar L para que la distancia BC obtenida sea igual a la dada a. Para expresar que BC = a, escribimos:
Para eliminar la raíz hacemos
El factor que nos interesa es el último, el primero ha aparecido al elevar al cuadrado, observemos que en él no aparece a). Entonces el polinomio del cual t es solución es:
Es un polinomio de grado 6, en general sus soluciones no serán construibles con regla y compás. Aquí sólo vamos a comprobar que en un caso particular el polinomio no es soluble por radicales, por lo que tampoco lo será el polinimo general.
Usamos la teoría expuesta por Titus Piezas III en Solving Solvable Sextics Using Polynomial Decomposition. La idea clave de este artículo es que si un polinomio de grado seis con coeficientes racionales es resoluble por radicales, entonces una determinada resultante de grado 15 debe factorizarse.
Ahora consideramos el ejemplo con m=1, a=4, wa=3.
Pedimos a Mathematica que halle sus seis soluciones:
Después hacemos:
Aquí RootReduce da el polinomio mínimo para el número algebraico t1+t2. Este polonomio coincide con la resultante de grado 15 que aparece en el documento de Titus Piezas III. Podemos ver que se trata de un polinomio de grado 15, por lo que nuestra ecuación de grado seis no es soluble por radicales. Si el resultado hubiera sido de grado menor, entonces el polinomio de grado seis hubiera sido soluble por radicales.
Para encontrar un valor apoximado de las soluciones de nuestra ecuación
hacemos: