Propuesto por Francisco Alcubilla, profesor de Estrategia territorial. Madrid. Problema 347 Construir un triángulo conocidos la longitud del lado a, el ángulo B y la medida de la longitud de la bisectriz interior Wa ó del otro vértice Wc Alcubilla, F. (2006): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (20 de octubre de 2006) |
|
SOLUCIÓN para wa |
|
En primer lugar resolveremos el caso en el que se conoce la bisectriz del ángulo A. Plantearemos la solución por medio de un lugar geométrico; para ello prescindiremos de momento del valor wa..
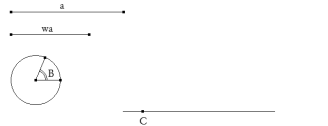
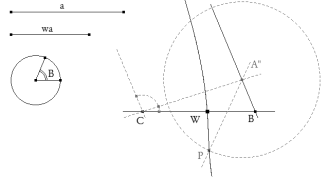
Introducimos los datos y dibujamos el vértice C sobre una recta cualquiera que será el lado BC.
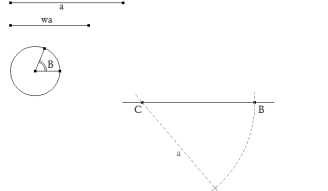
Con centro en C trazamos un arco de radio A que corta a la recta en el vértice B.
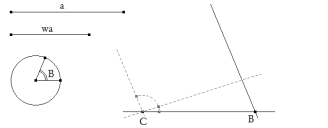
Con centro en B, rotamos la recta BC un ángulo B y obtenemos la recta soporte del lado BA. Trazamos por C una recta cualquiera, limitada por BC y una paralela al lado BA.
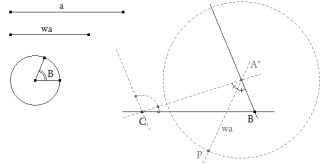
La recta cualquiera por C corta al lado BA en A”. Por A”, se traza la bisectriz de ∠BA”C. Con centro en A” trazamos un círculo de radio wa que corta a la bisectriz en el punto P. Si P estuviera sobre BC, tendríamos la solución buscada; en general no es el caso.
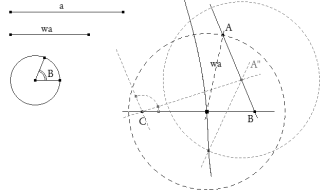
Trazamos con CABRI II plus el lugar geométrico del punto P al variar la recta por C. Este lugar corta a BC en W que es el punto solución.
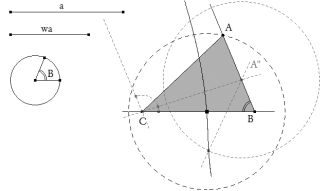
Trazamos, con centro en W, un círculo de radio wa que encuentra a BA” en el vértice A.
Trazamos ABC el triángulo solución. |
|
SOLUCIÓN para wc |
|
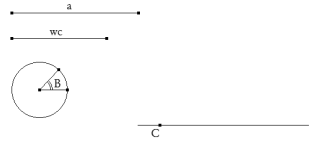
Resolveremos ahora el caso en el que se conoce la bisectriz del ángulo C. Plantearemos la solución por medio de la construcción directa introduciendo los datos paso a paso.
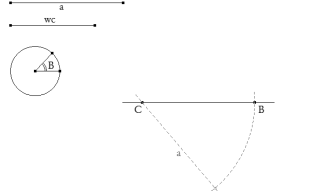
Introducimos los datos y dibujamos el vértice C sobre una recta cualquiera que será el lado BC.
Con centro en C trazamos un arco de radio A que corta a la recta en el vértice B.
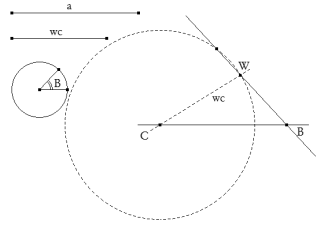
Con centro en B, rotamos la recta BC un ángulo B y obtenemos la recta soporte del lado BA. Trazamos por C un círculo de radio wc que corta en W al lado BA.
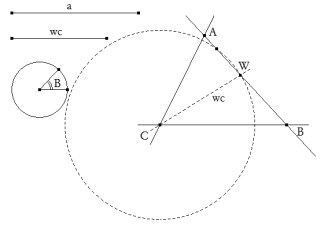
Trazamos ahora la simétrica de la recta BC con respecto a la bisectriz CW que cota a BW en el vértice A.
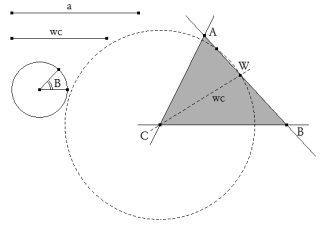
Trazamos ABC el triángulo solución.
El círculo con centro en C y radio wc que corta en en segundo punto al lado BA; con este segundo punto construiríamos una segunda solución. |