De investigación

Propuesto por de Juan Carlos Salazar, profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz).

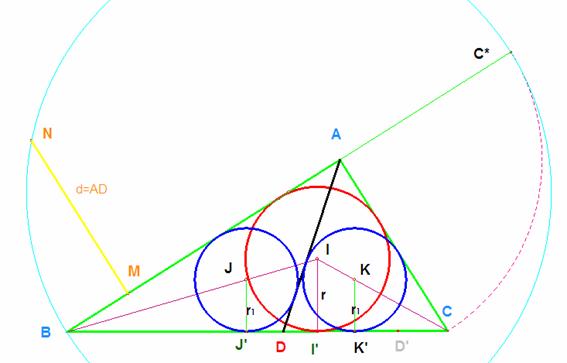
Problema 351.- En el triángulo rectángulo ABC(<A=90º) con inradio r se traza la ceviana AD de tal forma que los inradios de ABD y ADC son iguales a r₁. Probar que: 1/r₁=1/r + 1/AD.

Salazar, J. C. (2006). Comunicación personal.

Solución.-

En el problema 346, en una situación más general que esta, con un triángulo arbitrario ABC probamos que

(1)

y también que

d² =p(p-a) (2)

El triángulo ABC es rectángulo en A, por ello el radio del incírculo r es igual al valor p-a y la expresión (2) queda ahora

d² = pr (3)

Usando (1) y (3) obtenemos =

que es la expresión que deseábamos encontrar.

d es el lado del cuadrado de igual área que el triángulo.