Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 352

Sean T y T´dos triángulos rectángulos distintos, de hipotenusas a,a´,
y, catetos b,c, b´,c´, respectivamente.
Probar que aa´(bc´+b´c)= aab´c´+ a´a'b c si y sólo si los
triangulos T y T´ son semejantes.

Romero, JB. (2006): Comunicación personal

Solución de Ricard Peiró:

Supongamos els triángulos T y T’ semejantes entonces:

,          (1)

 esta igualdad es cierta si y sólo si:

           

         

        

Aplicando (1)

     

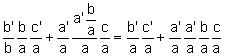
Supongamos que  y los triángulos T y T’ son rectángulos:

Entonces:

Entonces   o bien

Si ,  y por ser los dos triángulos rectángulos T y T’ son semejantes.

Si ,  por ser los dos triángulos rectángulos T y T’ son semejantes.