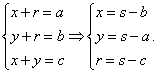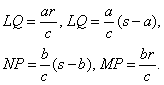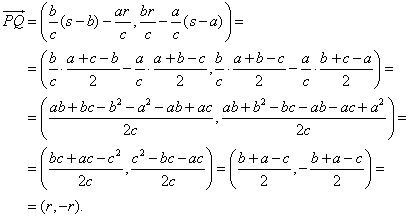En primer
lugar, aunque son muy conocidas, calculamos las distancias de los vértices
a los puntos de la circunferencia inscrita.
siendo s = (a + b + c)/2. Esta fórmula es válida para un triángulo cualquiera, aunque en el caso del triángulo rectángulo la distancia r es también el radio de la circunferencia inscrita.
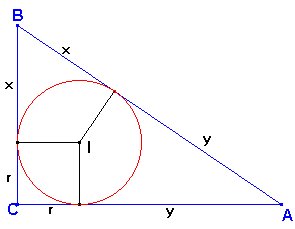
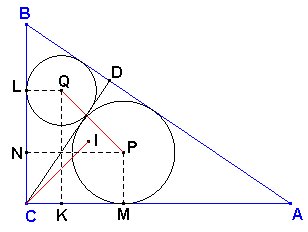Ahora,
si trazamos la altura CD, se forman los triángulos rectángulos
BCD y ACD, ambos semejantes a ABC. Las longitudes
AD, BD y CD son fácilmente calculables:
Observando que los triángulos CBD y ACD se obtienen al aplicar a ABC semejanzas con razones círculos inscritos en ACD y BCD pueden hallarse usando semejanzas de razones a/c y b/c, el radio de los círculos inscritos a estros triángulos será ar/c y br/c, respectivamente.
Entonces, en la figura tenemos:
Considerando a C el origen de coordenadas y a CA y CB los ejes, tenemos:
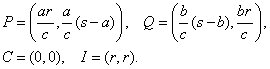
Una vez conseguidas las coordenadas cartesianas podemos comprobar que los vectores PQ y CI son perpendiculares y tienen el mismo módulo.
