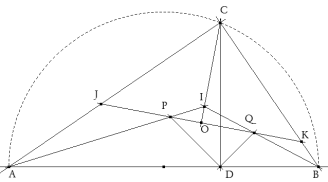
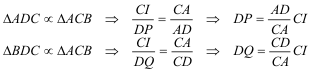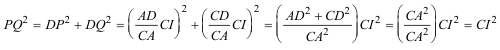De investigación. Problema 353 En un triángulo rectángulo ABC, recto en C, sea CD una altura. Los círculos de centros P, Q e I están inscritos en los triángulos
ACD, BCD y ABC, respectivamente. Demostrar que el segmento PQ es igual al segmento CI y es perpendicular a él.
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (5 de noviembre de 2006) |
|
SOLUCIÓN |
|
Resolveremos las cuestiones observando la figura trazada a partir del enunciado
El triángulo ADC tiene un ángulo recto y un ángulo común A con el triángulo rectángulo ACB, ADC y ACB son semejantes.
Con lo que hemos deducido la igualdad
Observando los ángulos de la figura y trabajando con ángulos dirigidos (módulo π) tenemos
Pero además
Y como los ángulos son menores que π
Entonces CO es perpendicular a KJ y por tanto CI es perpendicular a PQ. |