De investigación

Problema 353

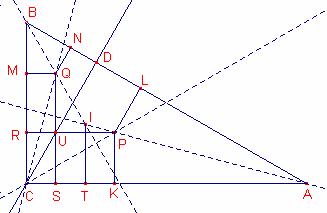
En un triángulo rectángulo ABC, recto en C, sea CD una altura.

Los círculos de centros P, Q e I están inscritos en los triángulos ACD, BCD y ABC, respectivamente.

Demostrar que el segmento PQ es igual al segmento CI y es perpendicular a él.

Campo, S. (2005) Métodos sintéticos de la geometría. Edición de autor. Salamanca. (p.22)

Solución de Ricard Peiró:

Los triángulos , ,  son rectángulos y semejantes.

En un triángulo rectángulo el radio de la circunferencia inscrita es igual al semiperímetro menos la hipotenusa.

Sea  el radio de la circunferencia inscrita al triángulo .

Sea  el radio de la circunferencia inscrita al triángulo .

Sea  el radio de la circunferencia inscrita al triángulo .

.

.

.

Por ser K punto de tangencia de la circunferencia inscrita del triángulo :

.

Por ser M punto de tangencia de la circunferencia inscrita del triángulo  :

.

Sea R la proyección de P sobre el lado a. Sea S la proyección del Q sobre el lado b.

Sea U la intersección de los segmentos , .

Probemos que  i que .

Los triángulos rectángulos  tienen los catetos iguales y los catetos correspondientes perpendiculares entonces las hipotenusas son iguales y perpendiculares, es decir,  y perpendiculares.

Prueba con Cabri:

Figura barroso353.fig

Applet created on 2/11/06 by Ricard Peiró with CabriJava