Solución de : Correa Pablo Ariel. Profesor de la ESB Nº42. Buenos Aires, Argentina.

Problema 354

Teorema de Euler

327 En todo triángulo ABC, la distancia d del centro de la circunferencia inscrita cuyo radio es r, al centro de la circunscrita cuyo radio es R, está dada por la relación dd= R(R-2r)

Frère Gabriel Marie, (1820-1891). Exercices de géométrie, comprenant l'esposé des méthodes géométriques et 2000 questions résolues par F. G.-M5. ed.:  3 p. L., [iii]-xxiv, 1302 p. diagrs. 22 cm. Tours, A. Mame et fils; [etc., etc.] 1912.(p. 173)
Casey, J. (1888) A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples, 6th ed. Dublin: Hodges, Figgis, & Co., 1888.(pp. 74-75)
Johnson, R. A.(1929) Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, (pp.186-187)
Altshiller-Court, N. (1952) College Geometry: A Second Course in Plane Geometry for Colleges and Normal Schools, 2nd ed., rev. enl. New York: Barnes and Noble, (pp. 85-86),
Lidski , V. y otros (1.978): Problemas de Matemáticas Elementales. Editorial Mir. Moscú (p.57)
Izquierdo, F. (2005): Fórmulas y propiedades geométricas. Edición de autor.Madrid.
Fernando Izquierdo Asensi es Doctor Ingeniero de Cosntrucción, y ex Profesor Titular de la Escuela Técnica Superior de Arquitectura de Madrid.
Ha dado su autorización al director de la revista. Se agradece su atención.

 

 

 

 

 

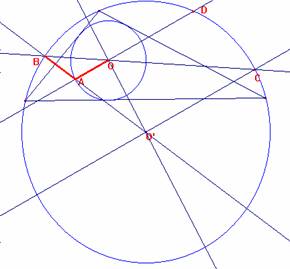
Descripción de la construcción:

 

1) Determinamos un  triángulo y construiremos la circunferencia inscripta y circunscripta llamando O y O’al incentro y circuncentro respectivamente.

2) Trazamos la recta OO’ y dos rectas perpendiculares a la misma por los puntos O y O’.

3) Si llamamos A a uno de los puntos de intersección de la circunferencia inscripta con una de las rectas anteriores que contiene al incentro,  tenemos que el triángulo O’OA es rectángulo de catetos OO’ = d y  OA = r.

4) Construimos la recta O’A y denotamos con B a uno de los puntos de intersección de esta recta con la circunferencia circunscripta al triángulo.

5) Los segmentos AB y AO son congruentes. Justificación:

 a) <OCO’ = <COD por  ser alternos internos entre paralelas.

 b) <COD   = <BOA por ser opuestos por el vértice.

 c) <O’BC = <BCO’ por ser el triángulo BO’C isósceles.

 d) Por a, b y c tenemos que el triángulo ABO es isósceles, siendo AB = AO = r.

6) Entonces, AO’=BO’-BA o AO’= R-r.

7) Por último, tenemos que el triángulo AOO’ es rectángulo

    de catetos OO’ = d , OA = r e hipotenusa AO’= R-r.

     Del que se deduce: (R-r)2 = d 2 + r2 o d 2 = R ( R-2r).