De investigación. Problema 354 (Teorema de Euler)

327 En todo triángulo ABC, la distancia d del centro de la circunferencia inscrita cuyo radio es r, al centro de la circunscrita cuyo radio es R, está dada por la relación dd= R(R-2r)

Frère Gabriel Marie, (1820-1891). Exercices de géométrie, comprenant l'esposé des méthodes géométriques et 2000 questions résolues par F. G.-M5. ed.: 3 p. L., [iii]-xxiv, 1302 p. diagrs. 22 cm. Tours, A. Mame et fils; [etc., etc.] 1912.(p. 173)

Casey, J. (1888) A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples, 6th ed. Dublin: Hodges, Figgis, & Co., 1888.(pp. 74-75)

Johnson, R. A.(1929) Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, (pp.186-187)

Altshiller-Court, N. (1952) College Geometry: A Second Course in Plane Geometry for Colleges and Normal Schools, 2nd ed., rev. enl. New York: Barnes and Noble, (pp. 85-86),

Lidski , V. y otros (1.978): Problemas de Matemáticas Elementales. Editorial Mir. Moscú (p.57)

Izquierdo, F. (2005): Fórmulas y propiedades geométricas. Edición de autor.Madrid. Fernando Izquierdo Asensi es Doctor Ingeniero de Cosntrucción, y ex Profesor Titular de la Escuela Técnica Superior de Arquitectura de Madrid. Ha dado su autorización al director de la revista. Se agradece su atención.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (17 de noviembre de 2006)

SOLUCIÓN

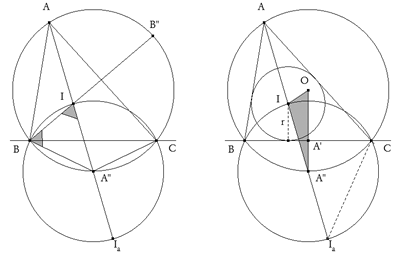
Trazamos los círculos; inscrito con centro I (intersección de las bisectrices) y circunscrito con centro en O (intersección de las mediatrices).

Un resultado preliminar

Observando la figura de la izquierda vemos que:

Sea A” el punto medio del arco BC. Entonces A”I=A”C=A”B=A”I_a (I_a centro del círculo ex-inscrito)

El triángulo A”BI es isósceles ya que el ángulo que hemos marcado en I es igual a (A+B)/2, el ángulo marcado en B tiene el mismo valor. El centro del círculo BIC es pues A”, punto medio del arco BC. El círculo BIC pasa también por I_a, ya que el cuadrilátero CBII_a es inscriptible.

Resultado final

Observando la figura de la derecha:

Si A’ es el punto medio del lado BC, la proyección de IA” sobre OA” es

Si nos fijamos en el triángulo OIA”

Pero del resultado preliminar

Podemos pues escribir el resultado buscado

La relación de Euler también puede escribirse como

Notas

Como I es siempre interior al círculo circunscrito, siempre se cumplirá que r≤R/2. Por tanto, r será máximo (de valor R/2) cuando ABC sea equilátero.

Si hubiéramos estudiado, en la figura, el triángulo OA”I_a, habríamos hallado con un razonamiento análogo

Bibliografía

Trajan Lalesco. La géométrie du triangle. Éditions Jacques Gabay 2003. ( 2e. Édition de Librairie Vuibert. 1952)