Teorema d’Euler: Distància entre l’incentre i el circumcentre

Siga el triangle i siguen R el radi de la circumferència circumscrita(de centre O) i r el radi de la circumferència inscrita(de centre I).

Aleshores:

Solución de Ricard Peiró i Estruch.

Demostració (partiendo de la bibliografia: COXETER, H.S.M., GREITZER, S.L.. “Retorno a la Geometría”. Colección “La Tortuga de Aquiles”. Ed Euler. 1994)

:

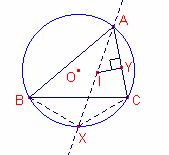Siga .

Siga la bisectriu a l’angle A.

Notem que X és el punt mig de l’arc BC.

Vegem que el triangle és isòsceles.

, per tant és isòsceles.

Aleshores:

Aplicant el teorema dels sinus al triangle

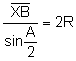
Aplicant raons trigonomètriques al triangle rectangle

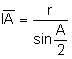
Apliquem la potencia del punt I respecte de la circumferència circumscrita al triangle

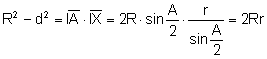
Aleshores,

Nota: , Aleshores tenim la desigualtat, .

Teorema:

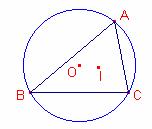Siguen r, R els radis de les circumferències inscrita i circumscrita d’un triangle qualsevol i siga la distància entre els centres de les dues circumferències anteriors.

Aleshores:

Demostració:

Pel teorema d’Euler sobre la distància entre l’incentre i el circumcentre:

on R és el radi de la circumferència circumscrita i r el radi de la circumferència inscrita.