Problema 354

Teorema d’Euler: Distància entre el incentro i el circumcentro

Sea el triángulo y sean R el radio de la circunferencia circunscrita(de centro O) y r el radio de la circunferencia inscrita(de centro I).

Entonces:

_.

Demostración: Solución de Ricard Peiró i Estruch.

Según Bibliografia: COXETER, H.S.M., GREITZER, S.L.. “Retorno a la Geometría”. Colección “La Tortuga de Aquiles”. Ed Euler. 1994

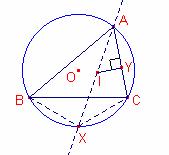
Sea .

Sea la bisectriz del ángulo A.

Notemos que X es el punto medio del arco BC.

Veamos que el triángulo es isósceles.

, por tanto es isósceles.

Entonces:

Aplicando el teorema de los senos al triángulo

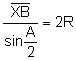
Aplicando razones trigonométricas al triángulo rectángulo

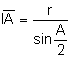
Apliquemos la potencia del punto I respecto de la circunferencia circunscrita al triángulo

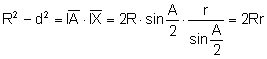
Entonces,

Nota: , Entonces tenemos la desigualdad, .

Teorema:

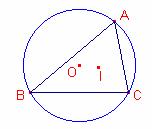Sean r, R los radios de les circunferencias inscrita y circunscrita de un triángulo cualquiera y sea la distancia entre los centros de las dos circunferencias anteriores.

Entonces:

Demostración:

Por el teorema de Euler sobre la distancia entre el incentro y el circumcentro:

donde R es el radio de la circunferencia circunscrita y r el radio de la circunferencia inscrita.

.

Bibliografia: COXETER, H.S.M., GREITZER, S.L.. “Retorno a la Geometría”. Colección “La Tortuga de Aquiles”. Ed Euler. 1994