De investigación .

 

Problema 354

Teorema de Euler

327 En todo triángulo ABC, la distancia d del centro de la circunferencia inscrita cuyo radio es r, al centro de la circunscrita cuyo radio es R, está dada por la relación d2= R(R-2r).

Frère Gabriel Marie, (1820-1891). Exercices de géométrie, comprenant l'esposé des méthodes géométriques et 2000 questions résolues par F. G.-M5. ed.:  3 p. L., [iii]-xxiv, 1302 p. diagrs. 22 cm. Tours, A. Mame et fils; [etc., etc.] 1912.(p. 173)

Casey, J. (1888) A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples, 6th ed. Dublin: Hodges, Figgis, & Co., 1888.(pp. 74-75)

Johnson, R. A.(1929) Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, (pp.186-187)

Altshiller-Court, N. (1952) College Geometry: A Second Course in Plane Geometry for Colleges and Normal Schools, 2nd ed., rev. enl. New York: Barnes and Noble, (pp. 85-86),

Lidski , V. y otros (1.978): Problemas de Matemáticas Elementales. Editorial Mir. Moscú (p.57)

Izquierdo, F. (2005): Fórmulas y propiedades geométricas. Edición de autor.Madrid.

Fernando Izquierdo Asensi es Doctor Ingeniero de Cosntrucción, y ex Profesor Titular de la Escuela Técnica Superior de Arquitectura de Madrid.

Ha dado su autorización al director de la revista. Se agradece su atención.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

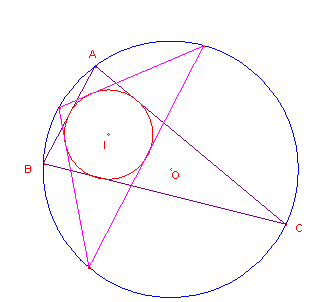
 Dibujamos un triángulo y sus dos círculos, inscrito y circunscrito. Después hacemos abstracción del triángulo y pensamos si habrá otro triángulo con igual círculo inscrito y circunscrito que aquél. Esta reflexión nos lleva al problema de los polígonos cerrados de Poncelet (nº 182) y concluimos que no hay uno: hay infinitos. Desde cualquier punto de la circunferencia circunscrita las tangentes a la inscrita determinan uno de ellos.

De aquí pasamos a buscar, entre todos ellos, cuál será aquél en el que resulte más sencilla la demostración de la fórmula de Euler.

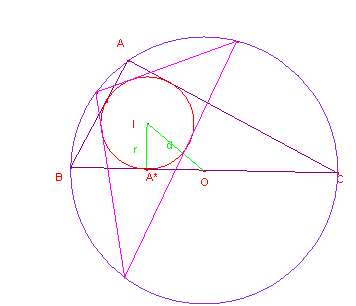
Parece evidente que esto sucederá en un triángulo rectángulo. El triángulo formado por incentro, circuncentro y punto de contacto del incírculo con la hipotenusa forman un triángulo rectángulo. A partir de ahí es bastante sencillo demostrar la fórmula.

 

r2 + (OA*)2 = d2;     r = p – a = ½ (–a + b + c)

 

OA*= R – BA* =  R – (p – b) = a/2 – ½ (a – b + c) = ½ (b – c).

Sustituyendo

 ==

==

=.

 

De otra parte,  R(R–2r)=a/2·(a/2 + a – b – c) =  y se demuestra el teorema.

 

La cuestión que se plantea ahora es ver si entre los infinitos triángulos que comparten esos círculos (inscrito y circunscrito) podemos encontrar uno que sea rectángulo. Esto sólo es posible cuando el circuncentro es exterior al triángulo. Pero si no hay uno rectángulo siempre se puede conseguir un isósceles: bastará tomar un vértice en el punto de corte del diámetro común con la circunscrita.

La demostración en este triángulo permitirá generalizarla a cualquier otro.

 

Elegimos un triángulo isósceles de base igual a 2 unidades y de altura h. Cualquier otro isósceles es semejante a éste.

 

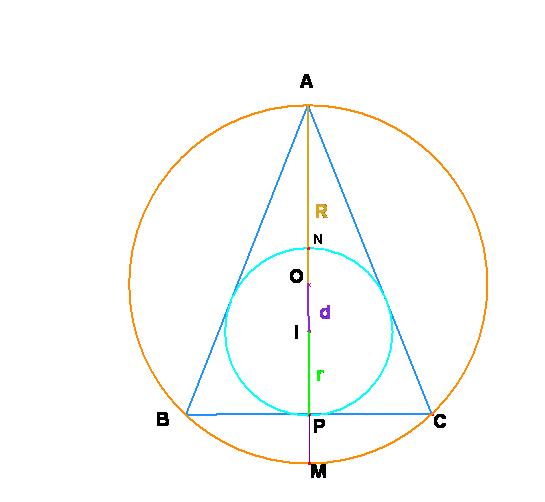
La relación a demostrar d2= R(R–2r) equivale a d2= (R – r)2 – r2,       

o bien,  r2= (R – r)2 – d2 = (R – r – d)·( R– r + d).

El semiperímetro de este triángulo es p =  y  su área es S=h, por tanto, el radio de la inscrita r= =. Para la circunscrita usamos la relación R= que da R= .  Del dibujo obtenemos

 

R – r – d = OM – IP – OI = MP   y   R – r + d = OA – (IN – IO)= NA.

 

Calculamos el producto de estos segmentos NA y MP.

 

La altura sobre P de los puntos A y N es h y 2r respectivamente, de ahí que el segmento NA mida h –.

(NA)2=.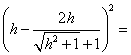

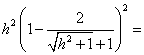
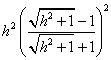La distancia de O a P es según el teorema de Pitágoras OP2 = OB2 – BP2 =R2 – 1 =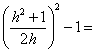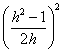, por tanto OP = , y de ello  MP = OM – OP =R– OP = 1/h.

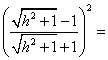
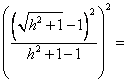
(NA)2·( MP)2 = 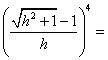r4.

Y de ahí NA · MP = r2 como queríamos demostrar, y con ello concluimos el teorema.

 

La fórmula demostrada d2 + r2 = (R–r)2  puede interpretarse como el teorema de Pitágoras para un triángulo de catetos d y r e hipotenusa R–r.

Dos circunferencias son la inscrita y la circunscrita a un triángulo cuando con esas magnitudes pueda formarse un triángulo rectángulo.

Este triángulo degenera en el caso del triángulo equilátero, pues ahí, R=2r y d es nula.