De investigación

Problema 354

Teorema de Euler

327 En todo triángulo ABC, la distancia d del centro de la circunferencia inscrita cuyo radio es r, al centro de la circunscrita cuyo radio es R, está dada por la relación dd= R(R-2r)

Frère Gabriel Marie, (1820-1891). Exercices de géométrie, comprenant l'esposé des méthodes géométriques et 2000 questions résolues par F. G.-M5. ed.:  3 p. L., [iii]-xxiv, 1302 p. diagrs. 22 cm. Tours, A. Mame et fils; [etc., etc.] 1912.(p. 173)

Casey, J. (1888) A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples, 6th ed. Dublin: Hodges, Figgis, & Co., 1888.(pp. 74-75)

Johnson, R. A.(1929) Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, (pp.186-187)

Altshiller-Court, N. (1952) College Geometry: A Second Course in Plane Geometry for Colleges and Normal Schools, 2nd ed., rev. enl. New York: Barnes and Noble, (pp. 85-86),

Lidski , V. y otros (1.978): Problemas de Matemáticas Elementales. Editorial Mir. Moscú (p.57)

Izquierdo, F. (2005): Fórmulas y propiedades geométricas. Edición de autor.Madrid.

Fernando Izquierdo Asensi es Doctor Ingeniero de Construcción, y ex Profesor Titular de la Escuela Técnica Superior de Arquitectura de Madrid.

Ha dado su autorización al director de la revista. Se agradece su atención.

Solución de William Rodríguez Chamache, profesor de geometría de la "Academia integral class" Trujillo- Perú

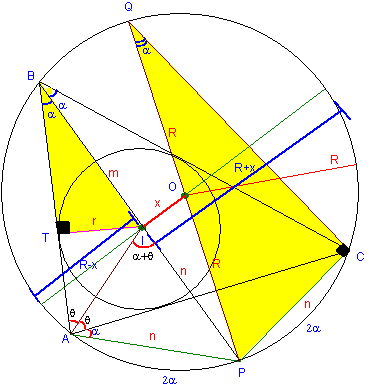
Los segmentos AP=PI=PC =n

Aplicamos el teorema de las cuerdas: m.n=(R-x)(R+x)

m.n = R²-x²……..   (1)

Luego en los triángulo semejantes BIT y QCP.

Se cumple.       m.n= 2Rr……. (2)

Igualando  (1) y (2) obtenemos: 2Rr= R²-x²

X²= R(R-2r)  Rpta.