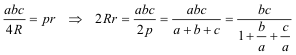De investigación. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 355

Dados los lados a>b>c ,( aquí se entiende como mayor o igual en todo el enunciado), del triángulo ABC, si R, es radio de su círculo circunscrito, y d, la distancia entre el incentro y circuncentro del triángulo, probar que :

0<d<(R^2- bc/3)^(1/2)

con la igualdad alcanzada en todos los miembros si y sólo si, el triángulo es equilátero.

Romero, J.B. (2006) : Comunicación personal

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (17 de noviembre de 2006)

SOLUCIÓN

Sea R el radio del círculo circunscrito y r el radio del círculo inscrito. Partiremos de tres resultados básicos:

a)           El resultado del problema 354: sol/sol354ped.htm

b)          El área del triángulo en función del radio del círculo circunscrito R

c)           El área del triángulo en función del radio del círculo inscrito r

Tomando b) y c)

si el triángulo es equilátero a=b=c y 2Rr=a²/3; pero en general a>b>c

y como hemos visto en las notas del problema 354 el máximo de r es R/2 que hace d=0, de donde