Problema 355

Donats els costats d’un triangle si R és el radi del cercle circumscrit i d la distància entre l’incentre i el circumcentre del triangle proveu que , la igualtat s’assoleix en ambdós membres si i només si el triangle és equilàter.

Solució Ricard Peiró:

L’àrea del triangle és on .

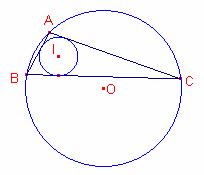Aleshores,

Pel teorema d’Euler de la distància entre l’incentre i el circumcentre:

Per a provar la desigualtat és suficient provar que

.

Per hipòtesi , aleshores,

.

Si el triangle és equilàter l’incentre i el circumcentre coincideixen aleshores:

on a és el costat del triangle

Si el triangle no és equilàter les desigualtats són estrictes.