Problema 355

Dados los lados del triángulo ABC, si R, es radio de su círculo circunscrito, y d, la distancia entre el incentro y circuncentro del triángulo, probar que :

0

con la igualdad alcanzada en todos los miembros si y sólo si, el triángulo es equilátero.

Romero, J.B. (2006) : Comunicación personal

Solució Ricard Peiró:

El área del triángulo es donde .

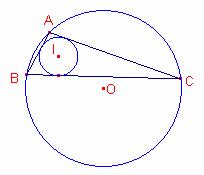Entonces,

Por el teorema de Euler de la distancia entre el incentro y el circuncentro:

Para probar la desigualdad es suficiente probar que

.

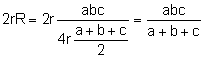Por hipótesis , entonces,

.

Si el triángulo es equilátero el incentro y el circuncentro coinciden entonces:

donde a es el lado del triángulo

Si el triángulo no es equilátero las desigualdades son estrictas.