Problema 356

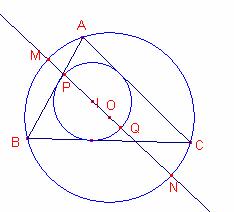
4.45 Tracemos los diámetros comunes a las circunferencias inscrita y circunscrita de un triángulo.

Sean M y N los extremos de estos diámetros y MP y NQ los segmentos del mismo comprendidos entre ambas circunferencias.

Demostrar que el radio de la circunferencia inscrita es media proporcional entre MP y NQ.

Prieto, M. ( 1992): Fundamentos geométricos del diseño en ingeniería. Aula documental de investigación. Madrid.

Con permiso de Manuel Prieto Alberca, autor del libro, a quien el director agradece su atención.

Solució Ricard Peiró:

Sea el triángulo  y O I el circuncentro y el incentro del triángulo.

Los diámetros comunes a les circunferencias inscrita y circumscrita pasan por O y I.

Siga  la distancia entre el incentro i el circuncentro del triángulo .

Por el teorema de Euler de la distancia entre el incentro y el circuncentro:

.

Aplicando la potencia del punto I respecto de la circunferencia circunscrita al triángulo:

Aplicando el teorema de Euler:

, es decir, el radio r de la circunferencia inscrita es media proporcional entre  y .

Con Cabri:

Figura barroso356.fig

Applet created on 17/11/06 by Ricard Peiró with CabriJava