De investigación

Problema 356

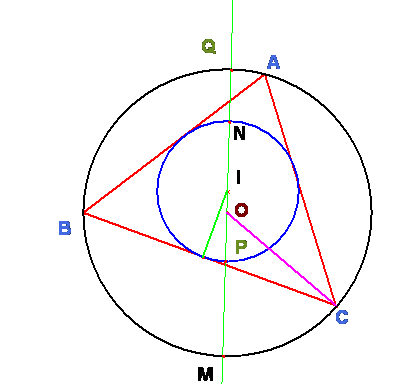
4.45 Tracemos los diámetros comunes a las circunferencias inscrita y circunscrita de un triángulo.

Sean M y N los extremos de estos diámetros y MP y NQ los segmentos del mismo comprendidos entre ambas circunferencias.

Demostrar que el radio de la circunferencia inscrita es media proporcional entre MP y NQ.

Prieto, M. ( 1992): Fundamentos geométricos del diseño en ingeniería. Aula documental de investigación. Madrid.

Con permiso de Manuel Prieto Alberca, autor del libro, a quien el director agradece su atención.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

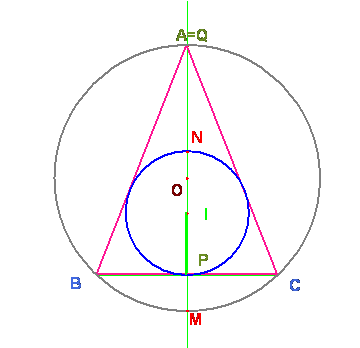
Los puntos M, N, P y Q sólo dependen de las dos circunferencias y no del triángulo ABC, por ello elijo como triángulo el isósceles con igual circunferencia inscrita y circunscrita. Para él se tiene que el punto Q coincide con A.

Tenemos que demostrar que MP·NQ = r². Esto es lo que hemos probado en el problema 354, donde el punto A es sustituido por Q.