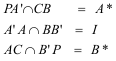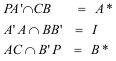De investigación. Propuesto por Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca
Problema 358 9.- Par les sommets A, B, C d’un triangle, on mène trois droites de même direction rencontrant le cercle cinconscrit G en A’, B’, C’. Soit P un point de G ; les droites PA’, PB’, PC’ rencontrent les droites BC, CA, AB en A*, B*, C*. Démontrer que ces points sont sur une même droite r. Quelle est la direction de cette droite ?
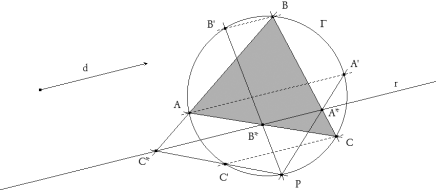
Por los vértices, A, B, C de un triángulo, se trazan tres rectas de igual dirección que reencuentran a la circunferencia circunscrita en A’, B’ y C’. Sea P un punto de G; las rectas PA’, PB’ y PC’ vuelven a encontrar a las rectas BC, CA y AB en A*, B* y C*. Demostrar que estos puntos pertenecen a una misma recta r. ¿Cuál es la dirección de esta recta ?
Commeau, J. .Cours Complet de Mathématiques. Géométrie. Masson et Cie, Éditeurs, 1957, Paris. (p. 71)
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de diciembre de 2006) |
|
INTRODUCCIÓN |
|
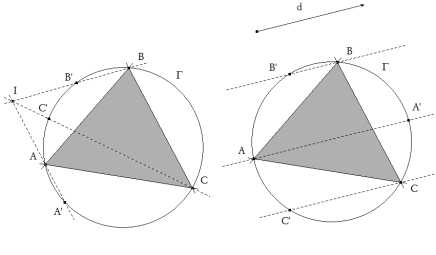
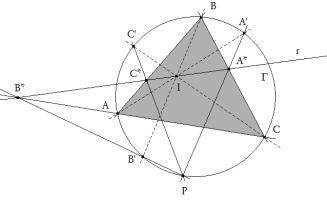
El hecho de trazar paralelas, a una dirección dada d, por los vértices ABC de un triángulo, equivale a unir los vértices del triángulo con el punto de infinito I de la dirección d. Por lo tanto, en principio, equivale a unir los vértices ABC con un punto I cualquiera de su plano y que para este enunciado particularizamos el punto I al caso del punto de infinito de una dirección dada d. Presentaremos este enunciado como caso particular de la PARTE III de una serie de enunciados vinculados en el que el punto I será un punto cualquiera del plano. PARTE I Dado un triángulo ABC y, en su plano, un punto I y una recta r que pasa por I. La recta r encuentra a los lados BC, CA, AB del triángulo respectivamente en los puntos A*, B*, C*. Las rectas AI, BI, CI cortan al círculo circunscrito Γ en A’, B’, C’. Demostrar que las rectas A’A*, B’B*, C’C* pasan por un punto P, situado sobre el círculo circunscrito Γ. PARTE II Dado un triángulo ABC y, en su plano, una recta r y un punto P de su círculo circunscrito. La recta r encuentra a los lados BC, CA, AB del triángulo respectivamente en los puntos A*, B*, C*. Las rectas PA*, PB*, PC* cortan al círculo circunscrito Γ en A’, B’, C’ respectivamente. Demostrar que las rectas AA’, BB’, CC’ pasan por un mismo punto I, situado sobre la recta r. PARTE III Dados dos triángulos ABC y A’B’C’ inscritos en un mismo círculo Γ, tales que las rectas AA’, BB’, CC’ pasan por un mismo punto I. Si P es un punto de Γ, se trazan las rectas PA’, PB’, PC’ que cortan a los lados BC, CA, AB respectivamente en A*, B*, C*. Demostrar que los puntos A*, B*, C* están sobre una misma recta r que pasa por I. La resolución la basaremos en el TEOREMA DE PASCAL que suponemos conocido y demostrado. |
|
SOLUCIÓN |
|
PARTE I Si P es el punto de encuentro de la recta A’A* con Γ, demostraremos que B’B* pasa por P. Sólo basta considerar el hexágono inscrito PA’ACBB’ cuyos puntos de intersección de los lados opuestos
están en línea recta de acuerdo al TEOREMA DE PASCAL. Del mismo modo veríamos que C’P pasa por C* si consideramos el hexágono PA’ABCC’. PARTE II Los puntos
siempre están en línea recta. Como el primero es A* y el tercero es B*, la recta que les une es r. Concluimos que r pasa por la intersección de AA’ y BB’, es decir BB’ pasa por I donde AA’ encuentra a r y lo mismo concluiríamos con CC’. PARTE III Considerando el mismo hexágono PA’ACBB’, vemos que los puntos A*, I, C* están también en línea recta. Por lo tanto los cuatro puntos A*, B*, C*, I están sobre una misma recta r.
Si I es el punto del infinito de la dirección dada d obtenemos la particularización a nuestro enunciado. Y como r pasa por I, será paralela a la dirección dada d. |
|
RESULTADOS ADICIONALES |
|
RESULTADO I Dados dos triángulos homológicos inscritos en un mismo círculo, si proyectamos desde un punto P cualquiera del círculo los vértices de uno sobre los lados del otro, los puntos obtenidos están en línea recta y esa recta pasa por el centro de homología. No es más que el resultado de la PARTE III. I es el centro de homología. RESULTADO II Dado un círculo y cuatro cuerdas AA’, BB’, CC’, DD’ que pasan todas por un mismo punto S; los puntos
están todos sobre una misma recta que pasa por S. Basta aplicar el RESULTADO I a los distintos triángulos que se forman. RESULTADO III Los simétricos de un punto del círculo circunscrito a un triángulo respecto a los lados de este triángulo están sobre una misma recta, que pasa por el ortocentro del triángulo. Basta tomar el ortocentro como punto I. BIBLIOGRAFÍA Georeges Papelier. Exercices de géométrie moderne.Éditions Jacques Gabay. Paris 1996. (Librairie Vuibert. Paris 1927) |