De investigación

Propuesto por Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

Problema 358

9.- Par les sommets A, B, C d’un triangle, on mène trois droites de même direction rencontrant le cercle circonscrit G en A’, B’, C’. Soit P un point de G ; les droites PA’, PB’, PC’ rencontrent les droites BC, CA, AB en A*, B*, C*. Démontrer que ces points sont sur une même droite r. Quelle est la direction de cette droite ?.

Por los vértices, A, B, C de un triángulo, se trazan tres rectas de igual dirección que reencuentran a la circunferencia circunscrita G en A’, B’ y C’. Sea P un punto de G; las rectas PA’, PB’ y PC’ vuelven a encontrar a las rectas BC, CA y AB en A*, B* y C*. Demostrar que estos puntos pertenecen a una misma recta r. ¿Cuál es la dirección de esta recta ?

Commeau, J. .Cours Complet de Mathématiques. Géométrie. Masson et Cie, Éditeurs, 1957, Paris. (p. 71).

Solución.- Vamos a sustituir la circunferencia circunscrita por una cónica cualquiera y en lugar de rectas de igual dirección, tomaremos rectas concurrentes en un punto Q. En esta situación demostraremos que los puntos A*, B* y C* son colineales y que la recta que los contiene r, también pasa por Q.

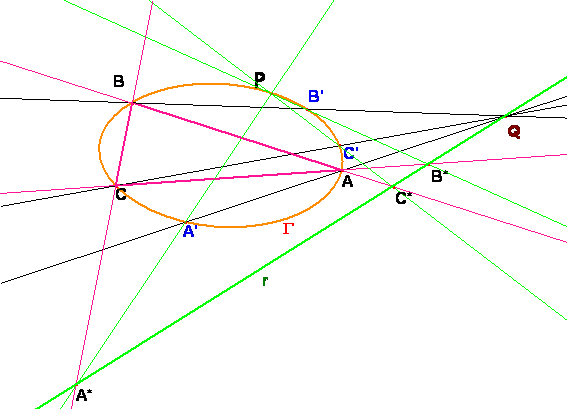
Consideremos el hexágono ACC’PB’BA inscrito en la cónica G. Aplicando el teorema de Pascal obtenemos que los puntos B*=AC∩PB’, Q=CC’∩BB’ y C*=AB∩ PC’ están alineados. Aplicando otra vez el teorema de Pascal, ahora al hexágono BCC’PA’AB, resulta la alineación de los puntos A*=BC’∩PA’, Q=AA’∩CC’ y C*=AB ∩ PC’. Por consiguiente los puntos A* y B* están sobre la recta que definen C* y Q.

Si el punto Q está en el infinito, las rectas concurrentes en él son paralelas. La recta que contiene a A*, B* C* es paralela a ellas.