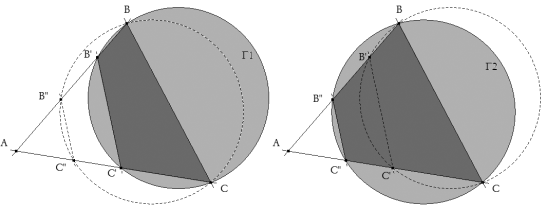
Para el aula. Problema 359

76.- Donat el triangle ABC. Siguen les circumferencies C1, C2 que pasen pels punts B, C i intersecten els costats AB, AC en els punts B’ C’ (la circumferència C1) i en els punts B’’ C’’ (la circumferència C2)

Proveu que els segments B’C’ y B’’C’’ són parallels.

76.- Dado el triángulo ABC. Sean las circunferencias C1, C2 que pasan por los puntos B, C e intersecan los lados AB, AC en los puntos B’ C’ (la circunferencia C1) y en los puntos B’’ C’’ (la circunferencia C2)

Demostrar que los segmentos B’C’ y B’’C’’ son paralelos.

Peiró, R. (1999): Problemes amb Cabri. Imprenta rápida Llorens, S.L. Valencia. Edición de autor. (p. 76)

Con permiso del autor. El director agradece la gentileza.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de diciembre de 2006)

SOLUCIÓN

Para establecer el resultado usaremos la siguiente proposición que consideramos conocida y demostrada:

EN UN CUADRILÁTERO INSCRITO EN UN CÍRCULO, LOS ÁNGULOS OPUESTOS SON SUPLEMENTARIOS

Si examinamos el círculo Γ1, según el enunciado, BCC’B’ es un cuadrilátero inscrito en este círculo y por tanto

Si examinamos el círculo Γ2, según el enunciado, BCC”B” es un cuadrilátero inscrito en este círculo y por tanto

Por lo tanto los triángulos AB’C’ y AB”C” tienen tres ángulos iguales y dos lados comunes y en consecuencia son homotéticos en una homotecia de centro A; de lo que deducimos que B”C” es paralela a B’C’ que es el resultado buscado.