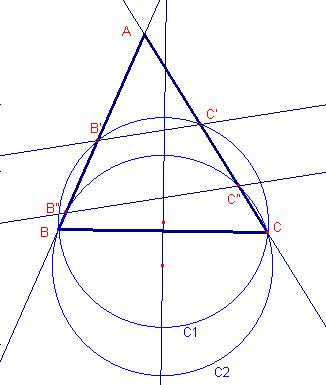
Problema 359

Dado el triángulo . Sean las circunferencias que pasan por los puntos B, C y intersectan los lados , en los puntos B’ C’ (la circunferencia ) y en los puntos B’’ C’’ (la circunferencia ). Probar que los segmentos i son paralelos.

Solución Ricard Peiró:

Los puntos B, C, C’, B’ forman un cuadrilátero inscriptible de la circunferencia .

Aplicando el teorema de Tolomeu los ángulos opuestos son suplementarios:

y .

Los puntos B, C, C”, B” forman un cuadrilátero inscriptible de la circunferencia .

Aplicando el teorema de Tolomeu los ángulos opuestos son suplementarios:

y .

Entonces,

, por tanto los segmentos i son paralelos.