Para el aula

Problema 359

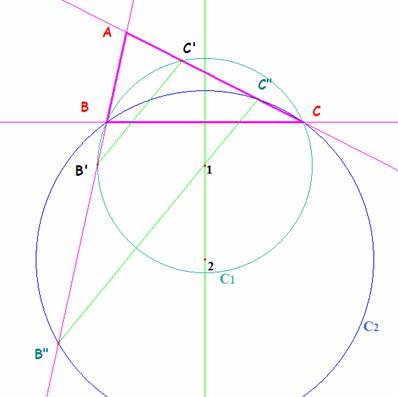
 76.- Donat el triangle ABC. Siguen les circumferencies C₁, C₂ que pasen pels punts B, C i intersecten els costats AB, AC en els punts B’ C’ (la circumferència C₁) i en els punts B’’ C’’ (la circumferència C₂)

Proveu que els segments B’C’ y B’’C’’ són parallels.

 76.- Dado el triángulo ABC. Sean las circunferencias C₁, C₂ que pasan por los puntos B, C e intersecan los lados AB, AC en los puntos B’ C’ (la circunferencia C₁) y en los puntos B’’ C’’ (la circunferencia C₂)

Demostrar que los segmentos B’C’ y B’’C’’ son paralelos.

Peiró, R. (1999): Problemes amb Cabri. Imprenta rápida Llorens, S.L. Valencia. Edición de autor. (p. 76)

Con permiso del autor. El director agradece la gentileza.

Solución.-

La potencia del punto A respecto de la circunferencia C₁ permite poner

AB·AB’=AC·AC’ (1)

La potencia respecto a C_{2 :} AB·AB”=AC·AC” (2) .

Dividiendo resulta que nos indica que los triángulos AB’C’ y AB”C” son semejantes y por ello los segmentos B’C’ y B”C” son paralelos. c.q.d.