Problema 360

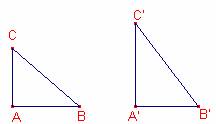
Sean T=ABC y T´=A´B´C´, dos triángulos rectángulos en A, y A´, respectivamente. Si, a,a´, son sus hipotenusas, b,c, b´,c´, sus catetos y S, S´, son sus áreas, respectivamente, probar que :

a) (a´c+ac´)²+(a´b+ab´)²+(bc´+cb´)²  - (aa´+bb´+cc´)² -16SS´>0,

con la igualdad alcanzada en la desigualdad si y sólo si T y T´ son semejantes

Solución Ricard Peiró:

a)

Si los triángulos T y T son rectángulos las áreas son:

, .

Aplicando el teorema de Pitágoras:

.

Si T i T’ son triángulos rectángulos semejantes si y sólo si, , si y sólo si

Entonces la igualdad se alcanza si y sólo si T y T’ son semejantes.