Problema 361.

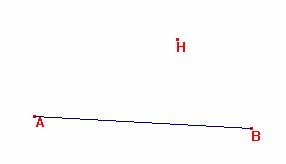
Dado en posición el lado AB y conocido el ortocentro H en posición, hallar C.

Alcubilla, F. (2006): Comunicación personal.

Solución del director.

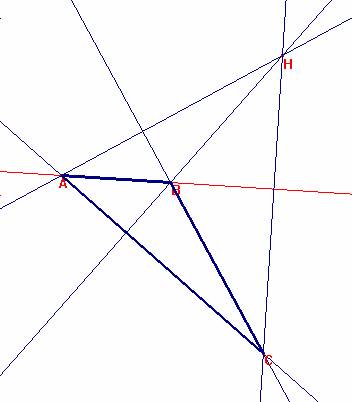
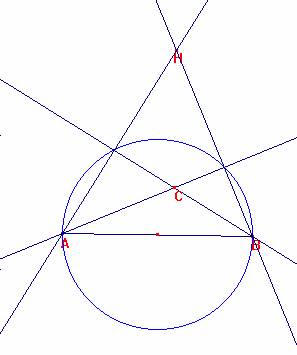
Sea la situación creada.

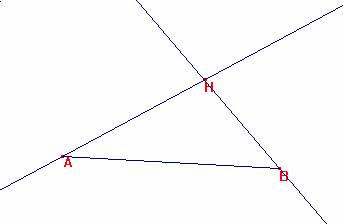
Tracemos las rectas AH y BH.

Tracemos por B la perpendicular a AH y por A la perpendicular a BH.

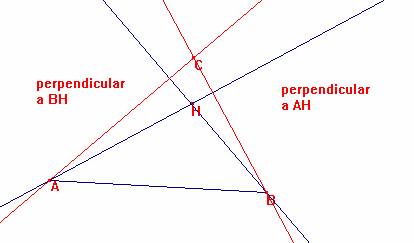
Se cortan en C.

Tracemos la recta CH.

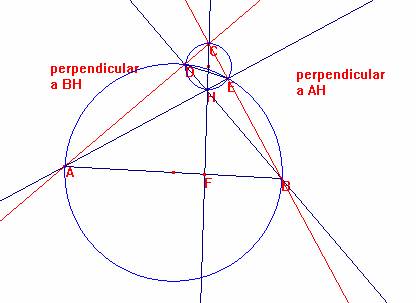
Los cuadriláteros CDHE por una parte y ADEB por otra son inscriptibles en circunferencias, por tener dos ángulos rectos en E y D.

Por propiedades de los ángulos inscritos, tenemos:

<DCH=<DEH, en el cuadrilátero CDHE por abarcar el mismo arco DH.

Por otra parte, <DAB=180-<BED por ser opuestos en el cuadrilátero ADEB.

Así al ser <DEC=180-<BED, es <DAB=<DEC.

Tenemos pues que <DCH+<DAB=<DCH+<CAF= <DEH+<DEC=<CEH=90º

Luego en el triángulo CFA tenemos que <CFA=180º- <CAF - <ACF=180º-90º=90º.

Así la recta AH es por tanto la tercera altura, cqd.

Podemos preguntarnos para qué puntos del plano la construcción es factible.

a) Si H está sobre el propio segmento AB o sobre la recta que lo contiene, se tiene que AH y BH se cortan dando como lugar geométrico la misma recta que contiene a AB y por tanto sería indeterminado. Las perpendiculares por A a BH y por B a AH serían paralelas, por lo que no habría triángulo.

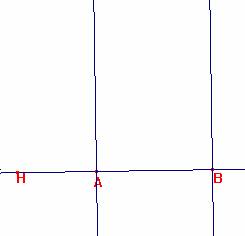
b) Si H se encuentra sobre la perpendicular a AB en A o en B,

Las perpendiculares a BH por A y a AH por B se cortan en B. Así el triángulo en tal caso es degenerado, ABB, pero, una vez construido el triángulo ABB, no existe el ortocentro, pues no existe la perpendicular desde A a BB, así pues podemos concluir que en tal caso el triángulo no existe.

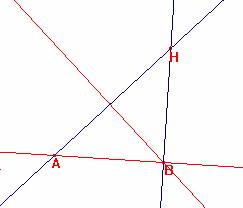
c) Si H es tal que el ángulo HAB o HBA son obtusos.

En tal caso ABC es también obtusángulo. La demostración de que CH es perpendicular a AB es mediante dos cuadriláteros concíclicos y se deja al lector. Es muy parecida al caso acutángulo estudiado anteriormente.

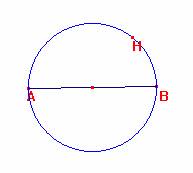
d) ¿Cuándo darán lugar AB y H a un triángulo rectángulo?

Debe estar H situado sobre la circunferencia de diámetro AB y por tanto coincide C con H, el vértice de ángulo recto.

f) ¿Cuándo darán lugar a un triángulo obtusángulo?

Ya vimos en c) un caso, si los ángulos HAB o HBA lo son.

Además si H es exterior a la circunferencia de diámetro AB, ABC es también

g) ABC será acutángulo si el ángulo AHB es obtuso y H está en el interior de la circunferencia de diámetro AB.

e) ¿Cuándo darán lugar a un triángulo equilátero?

Cuando AHB sea isósceles 30º 120º 30º.

Ricardo Barroso Campos

Departamento de Didáctica de las Matemáticas

Universidad de Sevilla