Problema 362.-

Un ángulo recto es igual a uno obtuso.

Rouse Ball, W. (1908): Recreaciones matemáticas y problemas de los tiempos antiguos y modernos. Segunda edición francesa. Segunda parte. Librería Científica Hermann. París. (p.2)

Demostrar que un ángulo recto es igual a un ángulo obtuso.- Sea un rectángulo ABCD; por el vértice A llevemos una recta AE exterior al rectángulo, igual a AB o DC y formando como muestra la figura, un ángulo agudo EAB con el lado AB. Tracemos CE y tomemos los puntos medios K y H de las rectas CE y CB. Las perpendiculares elevadas a estas rectas en los puntos K y H se encontrarán necesariamente en un cierto punto O debido a que CB y CE no son paralelas.

Tracemos OA, OD, OE, y OC.

Se tiene :

OA=OD y OE=OC.

Además, por construcción, AE=DC, pues los dos triángulos ODC y OAE son iguales teniendo los tres lados iguales y siendo <ODC=<OAE, o aún, <ODA+ 1 recto= <OAD+<DAE, de donde finalmente, <DAE=1 recto, pues por construcción, el ángulo DAE es obtuso.

Solución del director.

El razonamiento está basado en esta figura:

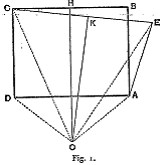
Pero realmente la figura es inexacta, ya que se trata de un giro del triángulo ODC con centro en O y ángulo COE. El segmento OE “queda” fuera del rectángulo y el ángulo <OAE es igual al <ODC. Con ello el razonamiento se hace erróneo.

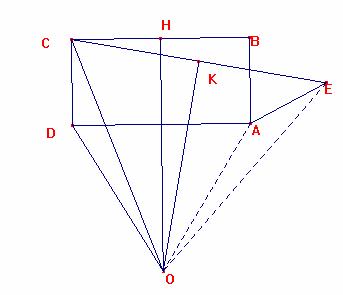
Ricardo Barroso Campos.

Didáctica de las Matemáticas.

Universidad de Sevilla.