Problema 363.-

Segundo sofisma.

Demostrar que un segmento de un lado de un triángulo es igual al lado completo.

Rouse Ball, W. (1908): Recreaciones matemáticas y problemas de los tiempos antiguos y modernos. Segunda edición francesa. Segunda parte. Librería Científica Hermann. París. (p.3)

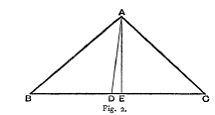
Segundo sofisma. Demostrar que un segmento de un lado de un triángulo es igual al lado completo. Sea ABC un triángulo cualquiera; para fijar ideas supongamos que el ángulo B es agudo y el ángulo A es mayor que el ángulo C.

Por el vértice A llevemos en el interior del triángulo la recta AD haciendo con el lado AB un ángulo BAD igual al ángulo C y abatamos la perpendicular AE sobre BC.

Los triángulos ABC y ABD son equiángulos y por tanto semejantes, por lo que se tiene que

[ABC]/[ABD]=AC²/AD²

Además, al tener la misma altura, la relación de áreas es igual a las de las bases, de donde se tiene la relación [ABC]/[ABD]=BC/BD

La comparación entre las dos relaciones nos da:

(1) AC²/AD² =BC/BD, o

AC²/BC=AD² /BD, o sea:

AC²=AB² + BC² -2BC BE

Y

AD²=AB² + BD² -2BD BE,

Y se llega, reemplazando en (1), a

(AB² + BC² -2BC BE)/BC= (AB² + BD² -2BD BE)/BD, de donde:

AB²/BC + BC – 2 BE =AB²/BD + BD – 2BE

o después de una simplificación y transposición,

AB²/BC -BD =AB²/BD – 2BC,

Y al fin,

(AB² –BD BC )/BC= (AB² – BD BC)/BD, de donde se deduce este resultado inadmisible, BC=BD.

Solución del director.

Casi todo el razonamiento es correcto, salvo la última deducción.

En el triángulo, si AD es tal que <BAD=<BCA, tenemos que los triángulos BAD y BCA son semejantes, por lo que AB/BD=CB/AB, luego es AB² – BD BC=0.

Así es cierto que (AB² –BD BC )/BC= (AB² – BD BC)/BD, pero al ser nulos los numeradores, no son iguales los denominadores, como deduce el autor.

Ricardo Barroso Campos

Departamento de Didáctica de las Matemáticas

Universidad de Sevilla