De investigación
Propuesto por Francisco Javier García Capitán, profesor del IES Álvarez Cubero (Priego de Córdoba).
Problema 364.- Dado un triángulo ABC y un punto P, consideramos los triángulos PBC, PCA, PAB y sus ortocentros Ha, Hb, Hc.
1. Los puntos Ha, Hb y Hc nunca están alineados, a menos que P esté sobre uno de los lados del triángulo ABC.
2. Las rectas AHa, BHb y CHc son concurrentes si y solo si P está en alguna de las alturas del triángulo ABC o en la circunferencia circunscrita al triángulo ABC.
3. El triángulo HaHbHc siempre tiene la misma área que ABC.
4. Cuando P está sobre la circunferencia circunscrita, el punto de concurrencia Q de AHa, BHb y CHc está sobre la circunferencia de los nueve puntos del triángulo ABC y los triángulos ABC y HaHbHc no son sólo perspectivos, sino que además HaHbHc es el resultado de aplicar a ABC una simetría central de centro Q. De hecho Q, es el punto medio del punto dado P y el ortocentro H del triángulo.
García, F. (2007): Comunicación personal.
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.-
1.- Si el punto P está sobre el lado BC, Hb y Hc han de estar situados sobre la altura desde A del triángulo. Por otra parte, en el triángulo degenerado PBC sus alturas (perpendiculares al segmento por cada punto) son tres rectas paralelas a la altura desde A. El ortocentro Ha es el punto del infinito de esta altura y así resultan Ha, Hb y Hc alineados.
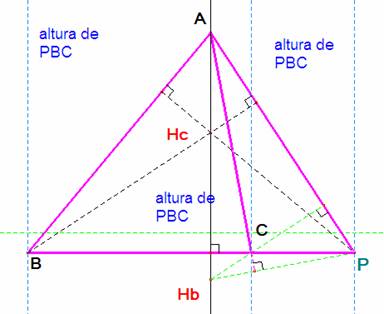
Si los ortocentros están alineados, vamos a demostrar que en ese caso también lo están los vértices del triángulo. Sea r la recta que contiene a A y a B, s la que contiene a los ortocentros y Q=r∩s
En general las rectas AHb y BHa son paralelas, pues ambas son perpendiculares al segmento PC. El hexágono AHbCHa BHc A tiene paralelos los pares de lados opuestos, aplicando el teorema de Pascal podemos asegurar que los seis vértices están sobre una cónica. Este teorema, ahora con el hexágono HaHbHcABCHa, nos sirve para concluir que la recta t, paralela a CHa por Q, es su recta de Pascal. Si llamamos Q’ al punto de encuentro de r y BC, Q y Q’ están en t (por ser la recta de Pascal) y también en r, por consiguiente Q=Q’ y con ello probamos la alineación de C con A y B.
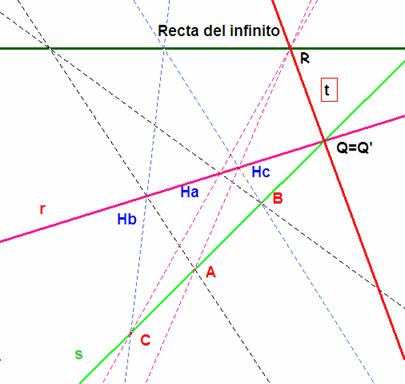
En esta situación si los ortocentros están alineados, el punto P ha de estar también alineado con ellos pues las alturas PHi son perpendiculares a la misma recta s.
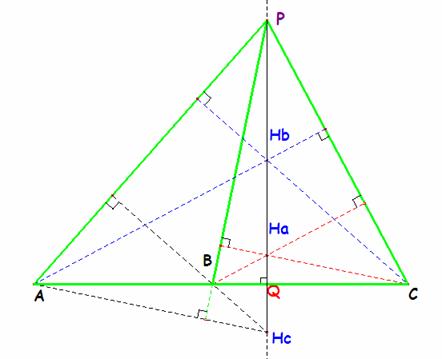
2.- a) Si el punto P está sobre la altura desde A, los ortocentros Hb y Hc yacen sobre la base a=BC pues la altura desde C del triángulo APC es BC; también lo es la altura desde B de APB.
Por último, la altura desde P de PBC es la altura desde A de ABC.
En conclusión, AHa, BHb y CHc concurren en Q, pie de la altura desde A de ABC.
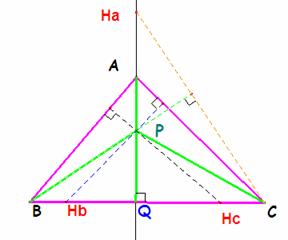
b) Vamos a suponer que P no está sobre ninguna altura, ni sobre ningún lado del triángulo.
Por los puntos P, A, B, C y Ha, pasa una única cónica G. Como Ha es ortocentro del triángulo PBC, según probamos en el problema nº 341 resulta que esta cónica es una hipérbola equilátera, que igualmente ha de contener a los otros ortocentros Hb y Hc. Podemos pues afirmar que hay una hipérbola equilátera que contiene al triángulo inicial y su ortocentro H, al triángulo de los ortocentros HaHbHc, así como al propio punto P que sirve para definir a éste último.
Supongamos ahora que el punto P se encuentra sobre la circunferencia circunscrita al triángulo.
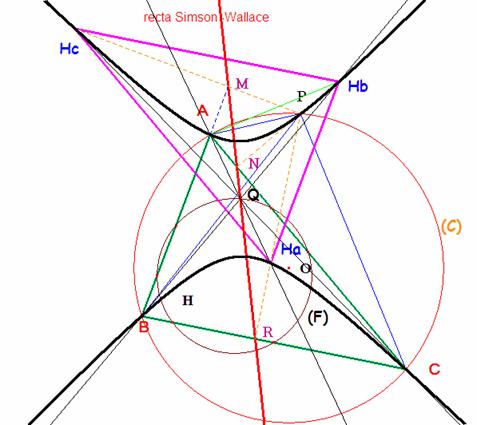
La recta de Simson-Wallace, definida por los puntos M=PHc∩AB, N= PHb∩AC y R= PHa∩CB, es el eje de la proyectividad sobre G en la que son homólogas las ternas (P A B) y (C Hb Ha). También lo es en la definida haciendo corresponder las ternas de puntos (P A C) y (B Hc Ha). Por todo ello, los puntos AHa∩CHa y AHa∩BHb también están en la recta de Simson-Wallace y por tanto AHa, BHb y CHa son concurrentes como se quería demostrar.
c) Veamos la proposición recíproca. Las rectas AHa, BHb y CHa son concurrentes en Q y el punto P no está sobre ninguna altura del triángulo. Los ejes de las dos proyectividades anteriores definidas sobre G por (P A B)à (C Hb Ha) y (P A C) à (B Hc Ha) van a resolver la cuestión.
El de la primera nos dice que los puntos N, R y Q están alineados. El de la segunda, que también lo están M, R y Q. Los cuatro puntos están alineados y tres de ellos son los pies de las perpendiculares desde P a los lados del triángulo ABC, luego P está en la c. circunscrita.
3.- Para probar esta parte, tomamos como ejes de coordenadas las asíntotas de esta hipérbola, como ya hicimos en el citado problema 341. Suponiendo que la hipérbola tiene por ecuación para xy=1, vimos que el triángulo PQR inscrito en ella, con vértices P(p,1/p); Q(q,1/q) y R(r,1/r) tiene por ortocentro el punto H(-1/(pqr),-pqr). Tomando aquí A(x1, 1/ x1); B(x2, 1/ x2); C(x3, 1/ x3) y P(x0, 1/ x0), tendremos para el triángulo ABC un ortocentro H=(-1/(x1 x2 x3), - x1 x2 x3).
El ortocentro Ha se obtiene sustituyendo x1 por x0 en la expresión de H.
Ha =(-1/(x0 x2 x3), - x0 x2 x3)
Hb se obtiene sustituyendo x2 por x0 en la expresión de H.
Hb=(-1/(x1 x0 x3), - x1 x0 x3)
Y Hc sustituyendo x3 por x0 en la expresión de H.
Hc=(-1/(x1 x2 x0), - x1 x2 x0)
El cálculo del área del triángulo HaHbHc en función de las coordenadas de los vértices es:
2Área (HaHbHc)=
Si en la segunda columna multiplicamos por x0 y en la segunda dividimos por x0, el determinante no varía, pero no depende ya del punto P elegido en el plano. Como lo que nos interesa es ver que es igual al área de ABC bastará que seamos capaces de probarlo en algún caso particular más sencillo. En el siguiente apartado del problema demostraremos que estos triángulos son congruentes cuando P se elige sobre la circunferencia circunscrita y así podemos dejar cerrada esta parte.
4.- En 2 obtuvimos que los triángulos ABC y HaHbHc son homológicos (con centro de homología Q). De ahí resulta de inmediato que también son homológicos los triángulos HaBHc y AHbC con el mismo centro de homología, pero con distinto eje. El eje de esta última homología está formado por los puntos de intersección de BHc y CHb (son paralelas), de BHa y AHb (también paralelas) y de HaHc y AC. De ello resulta que estas dos últimas también son paralelas y en consecuencia los triángulos no sólo son homológicos, son homotéticos. El paralelismo de HaHc y AC implica que PHb, perpendicular a AC sea una altura de HaHbHc y P su ortocentro.
Si HaC y HcA son paralelos, HaCAHc ¡es un paralelogramo! Tenemos así que ABC y HaHbHc son congruentes, (de lados paralelos e iguales). El centro de homología es el centro de homotecia y centro del paralelogramo. Y la homotecia, al no ser la identidad, es una simetría central. En esta transformación se transforma el ortocentro de un triángulo en el otro. El centro de simetría Q es por ello el punto medio del segmento PH (donde H es el ortocentro de ABC).
Sólo queda probar que Q está en la circunferencia de los nueve puntos.
En el problema nº 166 demostramos que el simétrico del ortocentro de un triángulo respecto del pie de una altura está sobre la circunferencia circunscrita. En el 233 demostramos esto mismo pero referido al pie de cada mediana. Como la circunferencia de los nueve puntos pasa por los pies de alturas y medianas, —suficientes puntos para determinarla completamente—, podemos decir que contiene los puntos medios de los segmentos con un extremo en el ortocentro y otro en la circunscrita. A los seis puntos anteriores pueden añadirse otros tres: los puntos medios de los segmentos que unen el ortocentro con los vértices. Esta circunferencia resulta ser el lugar geométrico de los puntos medios de los segmentos con un extremo fijo en el ortocentro de triángulo y el otro sobre la circunscrita.
Con esto queda demostrado que Q está en la circunferencia de los nueve puntos.