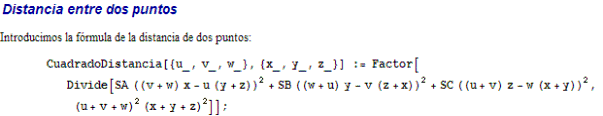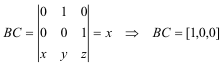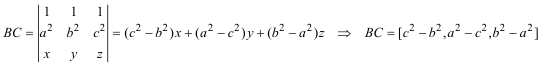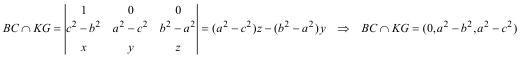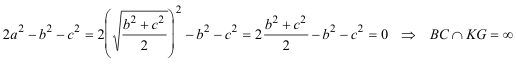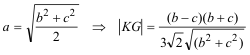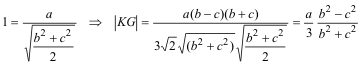De investigación. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 365.

Si el lado a de un triángulo es igual a la raíz cuadrada de la semisuma de los cuadrados de los otros dos lados, la recta KG que une el punto de Lemoine al centro de gravedad, es paralela a este lado e igual (a(b^2-c^2))/3(b^2+c^2).

De Alba, L (1901) Luis de Alba. Revista Trimestral de Matemáticas (Septiembre), p.112, Dección de cuestiones propuestas, número 11.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (18 de febrero de 2007)

DISCUSIÓN

Este es el tipo de problema que se maneja cómodamente con coordenadas baricéntricas.

La única función extraña a usar en baricéntricas es para hallar la distancia entre K y G

Fuente: Francisco Javier García Capitán.

apartado 7.1 de Paul Yiu: Introduction to the Geometry of the Triangle .

http://garciacapitan.auna.com/baricentricas/

Comprobaremos que la recta determinada por el lado en cuestión y la recta determinada por KG se cortan en el infinito, es decir son paralelas. La condición en baricéntricas para que un punto sea del infinito es que la suma de sus coordenadas sea nula.

Supondremos, sin pérdida de generalidad que el lado en cuestión es a

SOLUCIÓN

Hemos seleccionado como lado singular el lado BC. Recordemos

COORDENADAS BARICÉNTRICAS DE LA RECTA BC

Calculamos por medio de determinantes la ecuación de la recta BC

COORDENADAS BARICÉNTRICAS DE LA RECTA KG

Calculamos por medio de determinantes la ecuación de la recta BC

COORDENADAS BARICÉNTRICAS DE LA INTERSECCIÓN DE LA RECTA BC CON LA RECTA KG

De nuevo por medio de determinantes calculamos las coordenadas de la intersección de dos rectas

Sumando las coordenadas del punto de intersección tenemos

E imponiendo la condición del enunciado

Por lo tanto la recta BC (lado a) y la recta KG son paralelas

DISTANCIA ENTRE G Y K

Usando la fórmula del cuadrado de la distancia de Francisco Javier García Capitán obtenemos ∣KG∣

de donde, multiplicando y dividiendo por a

(c.q.d.)