|
Generalización del teorema de Simson.- Demostrar que: los pies de las perpendiculares bajadas de un punto O a los lados de un triángulo ABC forman una figura semejante a la terna A'B'C' de los puntos inversos de ABC en toda inversión de centro O. Deducir como corolario el teorema de Simson. |
|
Geometría Métrica. Puig
Adam, vol I. pág. 166. GOMEZ PUIG Ediciones, 15ª edición.
Madrid 1980.Propuesto por Saturnino Campo Ruiz.
|
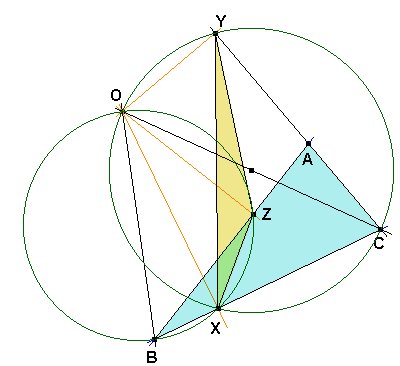
Llamemos X, Y, Z a los pies de las perpendiculares bajadas desde O a los lados BC, CA, AB, respectivamente. Observamos primero que el cuadrilátero BXZO es cíclico ya que los ángulos BXO y BZO son rectos. Lo mismo le ocurre al cuadrilátero OXCY.

Entonces tenemos que
ÐBXZ = 180º - ÐBOZ = 180º -(90º-ÐABO) = 90º + ÐABO,
ÐBXO = 90º,
ÐOXY = ÐOCY = ÐACO.
Entonces,
ÐYXZ = ÐBXZ - ÐBXO - ÐOXY = ÐABO - ÐACO.
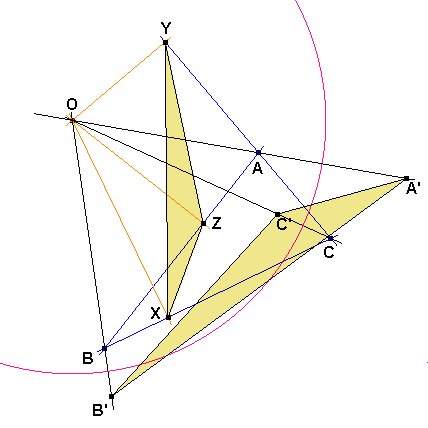
Ahora, si A', B', C' son los inversos de A, B, C respecto de una inversión con centro O, los triángulos ABO y ACO son semejantes a B'A'O y C'A'O respectivamente, por lo que tenemos
ÐYXZ = ÐABO - ÐACO = ÐB'A'O - ÐC'A'O = ÐB'A'C',
y lo mismo podemos hacer cíclicamente para los otros ángulos. Por tanto, XYZ y A'B'C' son semejantes.
Como caso particular, si el centro de inversión O pertenece a la circunferencia circunscrita entonces A', B', C' estarán alineados, y según acabamos de demostrar también lo estarán X, Y y Z. En consecuencia, obtenemos el teorema de Simson: Si O pertenece a la circunferencia circunscrita, entonces los pies de las perpendiculares bajadas desde un punto O están alineados.