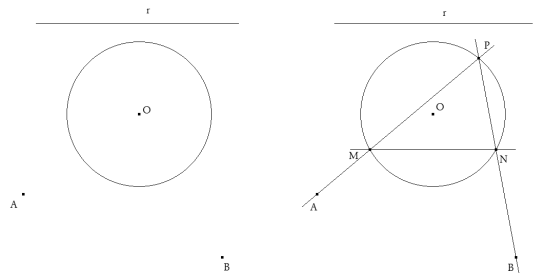
Problema 367

a) Inscribir, en un círculo de centro O, un triángulo MNP; donde el lado PM pasa por un punto dado A, el lado NP pasa por un punto dado B y el lado MN es paralelo a una recta dada r.

b) Aplicar el resultado anterior para obtener la resolución del problema de CASTILLON para círculo y triángulo.

Pedret, J.M. (2007):Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (14 de enero de 2007)

a) DISCUSIÓN

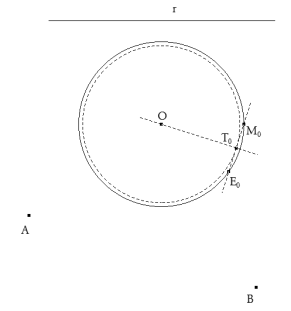
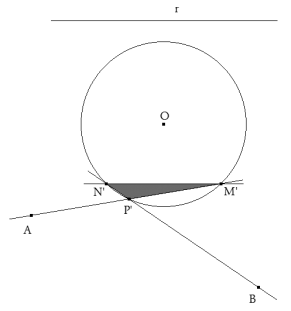
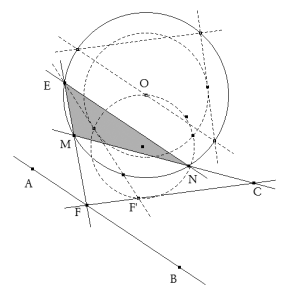
Como casi siempre, la mejor forma de atacar el problema es suponer que lo tenemos resuelto junto con su figura.

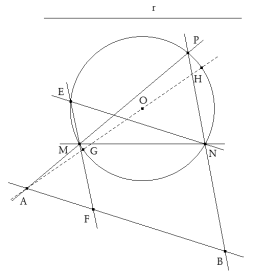
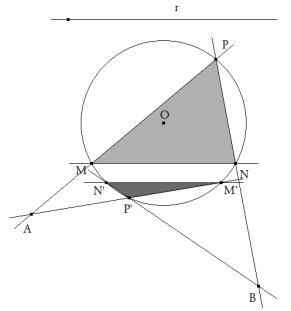
Por el vértice N, en principio desconocido, trazamos la paralela NE a la recta AB.

Por E trazamos la cuerda EM que corta en F a la recta AB. Si conociéramos F, el problema estaría resuelto, ya que el ángulo ENM, que es igual al ángulo formado por AB y la recta dada r, permite determinar la magnitud de la cuerda EM y entonces F nos permite determinar la posición de EM.

Para obtener el punto F, observemos que los ángulos MEN y MFA son iguales por ser alternos-internos, y los ángulos MEN y MPN son también iguales por estar inscritos en el mismo arco capaz; entonces los ángulos MPN y MFA son iguales y los triángulos APB y MFA, que tienen un ángulo igual y un ángulo común, son semejantes.

Por ser semejantes dichos triángulos, podemos escribir

ecuación que expresa la potencia conocida del punto A con respecto al círculo dado.

a) SOLUCIÓN

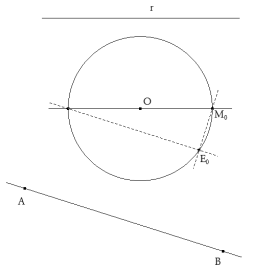
DETERMINACIÓN DE LA MAGNITUD DEL SEGMENTO EM

La magnitud de EM no es más que la cuerda del arco capaz del ángulo ENM, este ángulo es a su vez el que forma la recta determinada por AB y la recta dada r.

Para ello, trazamos por O el diámetro paralelo a la recta dada r, por uno de los extremos de dicho diámetro, trazamos una paralela a AB que corta al círculo en E₀. La magnitud buscada EM viene dada por el segmento E₀M₀, donde M₀ es el otro extremo del diámetro trazado.

DETERMINACIÓN DEL PUNTO F

Se traza por A un diámetro del círculo (vale cualquier secante) cuyos extremos son G y H; se cumplirá que

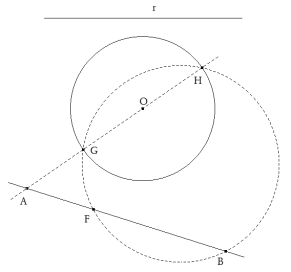
el círculo que pasa por G, H y B corta a AB en el punto F.

DETERMINACIÓN DE LA POSICIÓN DEL SEGMENTO EM

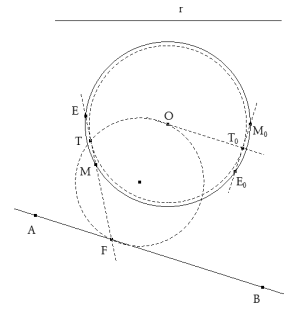
Cualquier cuerda de longitud EM será tangente al círculo de centro O y que pasa por T₀, donde T₀ es el punto medio de la cuerda E₀M₀.

Por lo tanto, la posición de la cuerda EM vendrá determinada por la tangente desde F al círculo de centro O y que pasa por T₀. El punto de tangencia es T. FT determina E y M sobre el círculo dado de centro O.

TRAZADO DE LA SOLUCIÓN

Determinado el punto M, el trazado de la solución es sencillo.

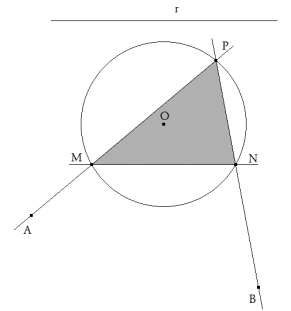
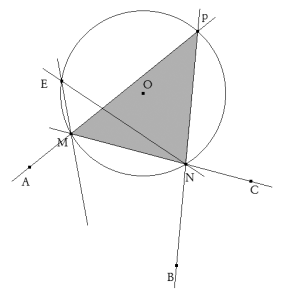
La recta AM contiene al lado MP que pasa por A. P es la otra intersección de AM con el círculo dado.

La recta BP contiene al lado PN que pasa por B. MN es paralelo a la recta dada r.

UNA SEGUNDA SOLUCIÓN

Como desde F podemos trazar una segunda tangente al círculo envolvente de las cuerdas EM, obtenemos una segunda solución.

Su punto de tangencia será T’ y FT’ corta al círculo dado en M’. Obtenido M’ podemos trazar la segunda solución.

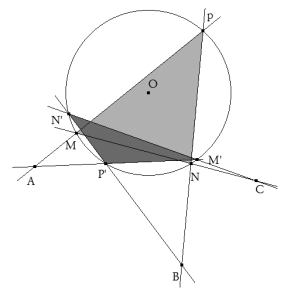
La recta AM’ contiene al lado M’P’ que pasa por A. P’ es la otra intersección de AM’ con el círculo dado.

La recta BP’ contiene al lado P’N’ que pasa por B. M’N’ es paralelo a la recta dada r.

LA SOLUCION FINAL DEL APARTADO a)

b) DISCUSIÓN DE LA APLICACIÓN AL PROBLEMA DE CASTILLON

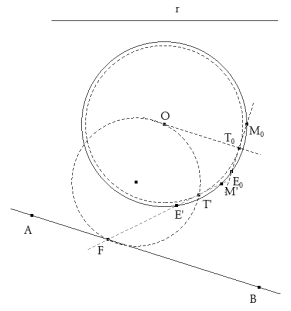
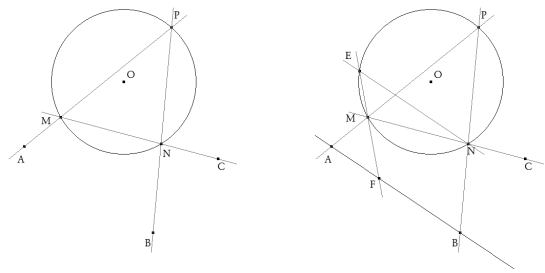
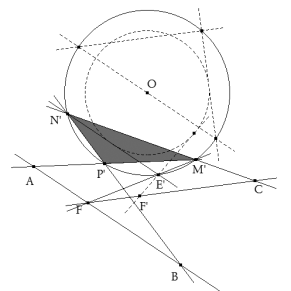
Supongamos que A, B, C son los tres puntos dados y que MNP es el triángulo buscado y que tenemos el problema resuleto (ver figura).

Llevamos NE paralela a AB y luego la cuerda EMF que encuentra a AB en F. Al igual que en el apartado anterior, podemos construir este punto F, después de lo cual, nuestro problema se reduce a inscribir un triángulo EMN en el círculo dado de centro O. Dos lados del triángulo pasan respectivamente por los puntos C, F y el tercer lado EN es paralelo a una dirección dada AB.

b) SOLUCIÓN DE LA APLICACIÓN AL PROBLEMA DE CASTILLON

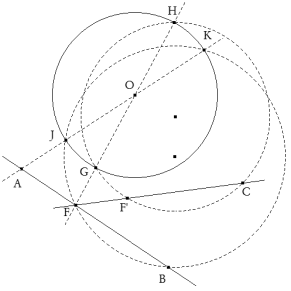
DETERMINACIÓN DEL PUNTO F

Por las mismas consideraciones que en el apartado a) sobre los ángulos, F será un punto de AB tal que

Si trazamos el diámetro del círculo que pasa por A, sus extremos son J y K, con lo que

así el círculo que pasa por J, K y B corta a AB en el punto F.

INSCRIPCIÓN DEL TRIANGULO EMN EN EL CÍRCULO DE CENTRO O

Como hemos visto en la discusión de b), este enunciado equivale al enunciado siguiente:

Inscribir, en un círculo de centro O, un triángulo EMN; donde el lado EM pasa por un punto dado F, el lado MN pasa por un punto dado C y el lado NE es paralelo a una recta dada AB.

Repetimos la construcción desarrollada en a) y obtenemos el triángulo EMN inscrito en el círculo dado de centro O. El punto F del apartado a) se convierte ahora en un punto F' sobre la recta FC; como hemos visto, trazando un diámetro de extremos G y H por el nuevo punto F que acabamos de determnar, el círculo por G, H y C corta a FC en F’. A partir de aquí seguimos sin cambios el resto del procedimiento desarrollado en el apartado a)..

DETERMINACIÓN DEL TRIÁNGULO MNP (Y LA SEGUNDA SOLUCIÓN M’N’P’)

El hecho de conocer el lado MN nos permite trazar el triángulo solución buscado.

Trazamos AM y BN que se cortan en P sobre el círculo. MN pasa por C.

El mismo procedimiento para la otra tangente desde F’ nos lleva al segundo triángulo E’M’N’ y de aquí al segundo triángulo M’N’P’

LA SOLUCION FINAL DEL PROBLEMA DE CASTILLON PARA CÍRCULO Y TRIÁNGULO