Problema 368
3.- ABC en un minuto
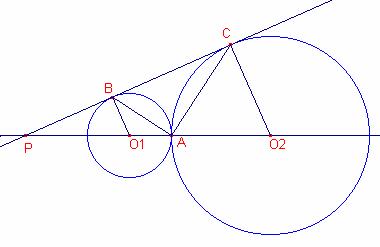
Dibuja dos círculos, uno pequeño y otro grande, tangentes exteriormente en el punto A. La tangente común a estos dos círculos toca al pequeño en B y al grande en C. Tienes un minuto para calcular el ángulo BAC. …
Tu turno:
Berrondo-Agrell, M. (2006) 101 enigmas de geometría, juegos divertidos para potenciar tu mente. Ediciones Ceac Barcelona.(p.11)
Solución de Ricard Peiró i Estruch.
Dibuja dos círculos, uno pequeño y otro grande, tangentes exteriormente en el punto A. La tangente común a estos dos círculos toca al pequeño en B y al grande en C. Tienes un minuto para calcular el ángulo BAC. …
Solución:
Sean 
los centros de les circunferencias de radios 
tangentes exteriores en el punto A.
Sea la recta r que une los centros .
Por ser de radio distinto, las circunferencias son homotéticas. Sea P el centro de homotecia y sea s la recta tangente a ambas circunferencias. La recta s pasa por el centro de homotecia P.
Sean B y C los puntos de tangencia.
Sea 
.
El triángulo 
es rectángulo 
.
Entonces, 
.
El triángulo 
es isósceles, 
.
Entonces,
.
El triángulo 
es rectángulo 
.
Entonces, 
.
El triángulo 
es isósceles, 
.
Entonces,
.
.
Calculemos el ángulo 
en función de los radios 
Sea 
Los triángulos , son semejantes. Aplicando el teorema de Tales:
.
Despejando la incógnita x:
.
:
.
Entonces,
.
Con Cabri:
Figurabarroso368n_b.fig
Applet created on 19/01/07 by Ricard Peiró with CabriJava
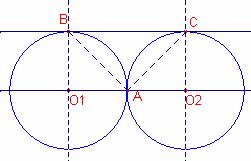
Notemos que si los círculos son del mismo radio r los puntos de tangencia B y C están en una recta paralela a la recta que une los centros de los círculos.
Entonces los triángulos 
son rectángulos y isósceles, por tanto,
.
Entonces, 
.
Notemos que por ser 
, 
.
Con Cabri:
Figurabarroso368p_b.fig
Applet created on 19/01/07 by Ricard Peiró with CabriJava