El director agradece la gentileza de Néstor Aguilera, Departamento de Matemática Universidad Nacional del Litoral, Santa Fe (Argentina) su gentileza a dar permiso para la publicación.

 

Problema 369.- Consideremos todos los segmentos que dividen al triángulo en dos áreas iguales.

Demostrar que la envolvente de los mismos son tres hipérbolas tangentes a las medianas y tangentes entre sí.

Enunciado a partir de  Aguilera N. (2007): El baricentro y la división en dos partes de igual área.

Solución.-

Acercamiento al problema.

 

Si dos triángulos AXX’, AYY’ tienen por área la mitad de la de ABC se verifica que  AX·AX’=AY·AY’ o bien , por tanto AXY’ AYX’ son semejantes y XY’ y X’Y son paralelos.

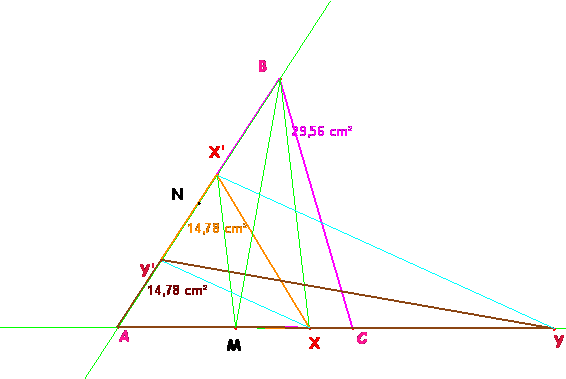
Un triángulo de área igual a la mitad de la de ABC es ABM con M punto medio de AC. Y también ACN. Para construir cualquier otro AXX’ con la misma propiedad, bastará tomar un punto cualquiera X en AC. Una paralela a  BX por M alcanza a AB en X’ y ya está hecho.

Esta construcción  puede entenderse fácilmente como una aplicación entre los puntos de la recta AC y los de AB. Las operaciones realizadas para asignar a un punto X el punto X’ (punto medio de un segmento, trazado de paralelas, cortar) son plenamente proyectivas. Podemos decir que así definimos una proyectividad entre esas dos rectas. Se corresponden en ella los puntos (M, C, X, Y)à(B, N, X’,Y’).

Según hemos observado anteriormente todos los pares de segmentos de la forma XY’ y X’Y son paralelos, eso significa que el eje de esta proyectividad es la recta del infinito del plano.

El lugar geométrico de las rectas XX’ que unen los puntos homólogos de una proyectividad (no perspectiva) entre dos rectas es una cónica tangencial o cónica dual, y esto es algo de lo que se nos pide en el problema. También tenemos que dos de las rectas que definen esta cónica son las medianas desde B y desde C.

Veamos algo más sobre estas cónicas.

 

 

Cónicas puntuales y cónicas tangenciales.

 

 

            Una cónica  proyectiva puntual es el lugar geométrico de los puntos comunes a los pares de rayos homólogos de dos haces proyectivos no perspectivos[1].

 

Si denotamos por P* y Q* los haces de rectas de vértices los puntos P y Q, la cónica viene definida por la aplicación           h: P* à Q*,    tal que h(PM) = QM.

 

 

 

 

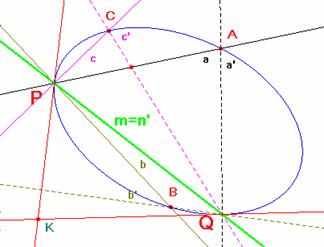
Para determinar la recta homóloga de una recta dada, se hace uso del centro proyectivo K de los haces.

Para la recta  que une los dos centros de los haces m = PQ, considerada como recta del primer haz, tiene como homóloga la recta m’= QK en el segundo; pero si se considera en el segundo haz, n’ =QP es homóloga de n = PK.

 

Así pues, la cónica definida por los puntos de intersección de dos haces centrados en P y Q contiene también los vértices de esos haces. De todo esto se concluye que una cónica puede definirse mediante 5 puntos: dos de ellos P, Q se toman como vértices y así queda fijada la proyectividad entre los haces P* y Q*.

Se puede demostrar que si se toman otros puntos como vértices para la proyectividad entre haces, la cónica definida es la misma.

 

Sobre cualquier recta x del haz sobre P hay dos puntos distintos de la cónica puntual, el punto P y el punto X=x∩x’ con x’ su homóloga en el haz sobre Q. La recta n= PK es una excepción ya que su homóloga es la recta n’ =QP y n∩n’=P.

De forma similar, en el haz sobre Q, sucede con la recta m’= QK. Es homóloga de la recta m = PQ y m∩m’=Q.

Una tangente a una cónica puntual es cualquier recta sobre la que hay únicamente un punto de la cónica. Se tiene pues, que la tangente a una cónica en uno de los vértices se obtiene uniéndolo con el centro de la proyectividad K: la tangente en P es la recta PK, la tangente en Q es QK.

 

 

            Una cónica  proyectiva tangencial es el lugar geométrico de las rectas que unen  a los pares de puntos homólogos de dos haces proyectivos de puntos no perspectivos.

 

            Cuando decimos haces de puntos hacemos referencia a las rectas base de la proyectividad.

            Sean r y s estas rectas. En general, sobre cualquier punto X del haz de puntos r hay dos rectas distintas de la proyectividad: la recta base r y la  recta x=XX’ donde X’ es el punto homólogo de X en s.

Construido el eje p de la proyectividad el homólogo de un punto U es el punto U’ construido proyectando desde un punto X’ de s sobre p y volviendo a proyectar éste último desde su homólogo X en r.

El punto S’=p∩s es homólogo del punto S =r∩s considerado como perteneciente a la primera.

S’ está en s y en s=SS’. Es un punto de contacto de la cónica tangencial definida por la proyectividad.

 

Si se considera que S  pertenece a s, es el homólogo del punto T de r. T está en r y también  en TT’=TS=r. T es otro punto de contacto de la cónica tangencial.

 

Una proyectividad entre dos rectas queda definida conociendo los homólogos de tres puntos distintos. Las rectas que unen estos homólogos junto con las dos rectas base de la proyectividad son los cinco elementos necesarios para que quede definida una cónica tangencial.

Dejamos al lector la comprobación de que esta cónica no varía si se eligen como bases otras dos rectas entre esas cinco.

 

Resolución del problema

 

            Según acabamos de ver, los puntos de encuentro del eje proyectivo con las rectas base r=AC,  s=AB son  puntos de contacto de la cónica  tangencial. Como el eje es la recta del infinito, deducimos que la cónica que estamos investigando es una hipérbola y que las rectas base son sus asíntotas (sobre ellas se encuentran, en el infinito, los puntos de contacto).

 

 

 

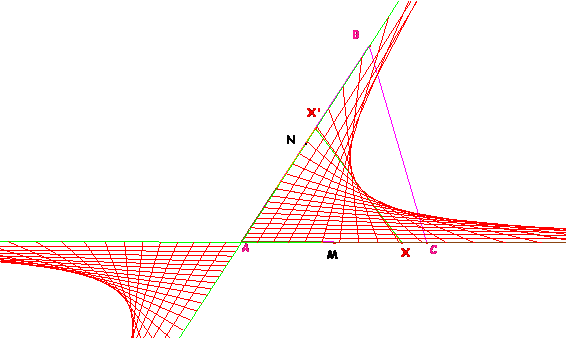
Si considerásemos los triángulos de área igual a la mitad del inicial tomando un punto sobre AC y otro sobre CB tendríamos igualmente, como envolvente de las rectas que unen esos puntos, otra hipérbola. Son tangentes a ella las medianas desde A y B.

Estas dos hipérbolas tangenciales comparten una tangente (la mediana desde B): son tangentes a ella, como se quería demostrar.

 

            Veamos por último, que estas hipérbolas, con una tangente común, son tangentes entre sí. Para ello vamos a calcular el punto de contacto que cada una de ellas tiene en la tangente común: mediana BM.  Las cinco rectas que definen la cónica cuyas asíntotas son AC y AB son, además de éstas, las medianas BM y CN y cualquier otra recta XX’ que una un par de homólogos.

 

Si llamamos a las rectas base r y s y después llamamos a, b y c a las otras tres, la proyectividad definida entre las dos primeras se obtiene haciendo corresponder los puntos    a∩r à a∩s;        b∩r à b∩s;    y por último  c∩r à c∩s.

Tomando r=BM, s=AB, a=AC, b=CN c=XX’, la proyectividad que define la cónica tangencial viene definida así:

 

 

 

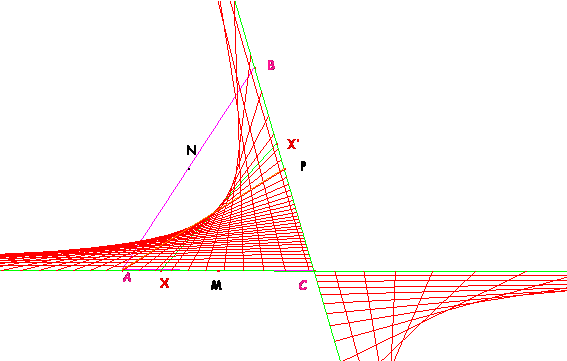
a∩r=M à a∩s=A;    b∩r=G à b∩s=N;      c∩r=Z à c∩s=Z’.

 

Se corresponden las ternas (M, G, Z)à(A, N, Z’).

El eje de esta proyectividad proporciona dos puntos de contacto de la cónica, uno en cada recta base. Sobre la recta s, que como ya sabemos es una asíntota, es su punto del infinito, y sobre r no sabemos: es el que estamos buscando. El dato del primer punto nos indica que el eje proyectivo es paralelo a la recta s=AB. Como sabemos que se corresponden (M, G, Z)à(A, N, Z’), deducimos que en este eje se debe encontrar el punto D=MN∩GA y por tanto se trata de la recta que pasa por D y es paralela a AB. Donde encuentre a la mediana BM será el punto T de contacto con esa tangente.

 

Para la hipérbola en la que AC y BC son asíntotas, el mismo procedimiento nos lleva a que el eje de la proyectividad entre BM y BC que define esta cónica hace los corresponder los pares (M, G)à(C, P) y es paralelo a la recta BC. Ha de pasar por E=MP∩GC y alcanza a la mediana BM en el punto de contacto de la hipérbola con ella.

Siendo M, N y P los pies de las medianas del triángulo, los puntos D y E son los puntos medios de los segmentos MN y MP, de ahí que los ejes de estas proyectividades concurran con la mediana BM en T punto medio de NP. Y con esto concluimos la tangencia de esas cónicas.

 

Se podría haber demostrado que T es el punto de contacto de esas hipérbolas con la mediana BM tangente a ambas apoyándose en un teorema (que no vamos a demostrar) según el cual el punto de contacto de una tangente a una hipérbola es el punto medio del segmento de tangente interceptada por las asíntotas.

 

            Una tercera hipérbola se obtiene considerando puntos en las rectas AB y BC. Así  pues tenemos que esas tres cónicas son tangentes a las medianas y tangentes entre sí en los puntos medios de las medianas D, E y T.

 

 

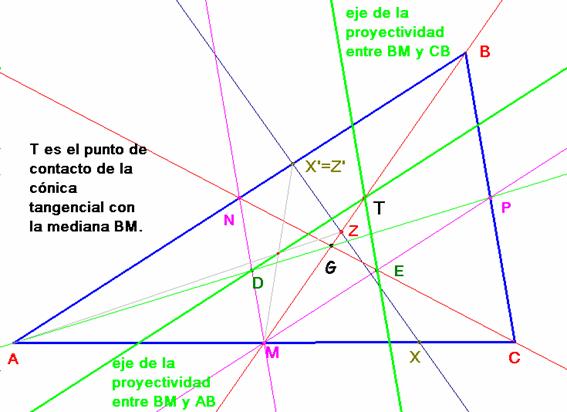
Construcción gráfica final

 

 

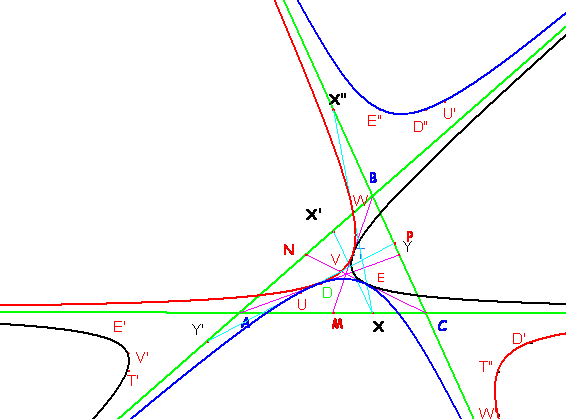
Vamos a obtener puntos suficientes de cada una de estas tres hipérbolas para dibujarlas y poder observar en el dibujo todas las propiedades demostradas.

Al ser asíntotas los lados del triángulo, los vértices son centros de cada una. El simétrico respecto del centro de un punto sobre la cónica proporciona otro punto de la misma. Tomando además la propiedad citada respecto a los puntos medios de los segmentos de tangente interceptados por las asíntotas, sólo un punto más es necesario (y con su simétrico respecto al centro ya nos sobran puntos) para poder dibujar las tres cónicas.

Se han tomado (X,X’), (X,X”), (Y,Y’) pares de puntos homólogos en las proyectividades que definen estas cónicas y sus puntos medios V, W y U cada uno perteneciente a una cónica. Con éstos puntos, los puntos medios de las medianas, D, E y T, y los simétricos respecto del centro de cada cónica disponemos de 6 puntos para su trazado.

 

 

Coordenadas cartesianas

 

Supongamos que tomamos como origen de coordenadas el punto A(0,0). El punto C(a,0) y el punto B(x0, y0). Si elijo X(t,0) sobre la recta AC, como extremo del segmento que divida al triángulo en dos partes de igual área; un cálculo bastante elemental proporciona para el otro extremo, sobre el lado AB, el punto X’= . De este modo el área de ABC es justamente el doble de la de AX’X. También podríamos haber buscado el punto X’ sobre BC.

El punto X varía sobre la recta soporte del lado AC. La ecuación de la recta determinada por X y X’ es

 

    (1)

 

Si F(x,y,t) =0 es la ecuación (1) de la familia de rectas dependiente del parámetro t, eliminando éste a partir de esa ecuación y de  obtenemos después de simplificar, la ecuación de la envolvente:

 

        (2)

 

Al tratarse de una ecuación polinómica de segundo grado deducimos que se trata de una cónica.

Para hallar los puntos del infinito tenemos que resolver .

Tomando m=y/x y dividiendo por x2 resulta my0 =m2x0. Resolviendo se obtienen las direcciones de las asíntotas, m=0 y m=y0/x0, que son precisamente las dos rectas donde se encuentran los puntos X y X’. (En la figura es la hipérbola dibujada en negro).

 El punto de tangencia en la mediana BM (con la hipérbola de rojo) es el punto T  y en la mediana CN (hipérbola azul) es el punto E de coordenadas . Puede comprobarse que ambos verifican la ecuación (2).

Y con esto damos por concluido el problema.

 


[1].- Si los haces son perspectivos, la cónica se reduce a un  par de rectas: el eje de la perspectividad y la recta que une los vértices de los haces.