De investigación

Propuesto por Francisco Javier García Capitán , profesor del IES Álvarez Cubero (Priego de Córdoba)

Problema 370

Sean ABC un triángulo en el que BC =(CA+AB)/2. Sean  I, N, G el incentro,
punto de Nagel y el baricentro,del triángulo ABC. Entonces:
a) El punto N está siempre en la mediatriz de BC.
b) IG es paralela a BC y además IG = |AB - AC|/6.
c) IN es paralela a BC y además GN =|AB - AC|/3.

García, F. (2007): Comunicación personal.

Solución del director

a)      Sea ABC el triángulo. Tomemos AB=4c, AC=4b; al cumplir las condiciones del enunciado, debe ser BC=2b+2c. Así el perímetro es s=6b+6c, y el semiperímetro es p=3b+3c.

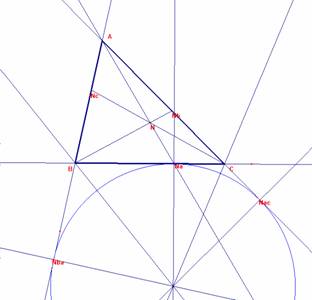
Tracemos la circunferencia exinscrita relativa al vértice A. Sean N_a el punto de tangencia con BC, N_ba el punto de tangencia con la prolongación de AB, N_ac con AC. 

Siendo BN_a=BN_ba =p-AB=(3b+3c)- 4c=3b-c. N_aC= BC-BN_a= (2b+2c)-(3b-c)=3c-b.

AN_c = p-AC=(3b+3c)-4b=3c-b,BN_c= AB-AN_c=4c-(3c-b)=b+c.

CN_b=p-CB=(3b+3c)-(2b+2c)=b+c, N_bA=AC-CN_b=(4b)-(b+c)=3b-c,

Así, CN_b=BN_c=b+c=BC/2.

Si trazamos una paralela por N_b a BC, cortará a CN_c en U

 

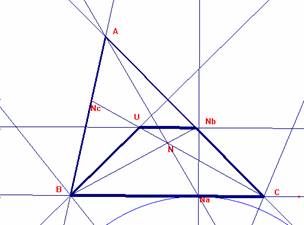
También si trazamos la circunferencia de centro C y radio CN_b=CM_a  y hacemos una tralación de vector , cortará a la paralela por N_b en U a CN_c.

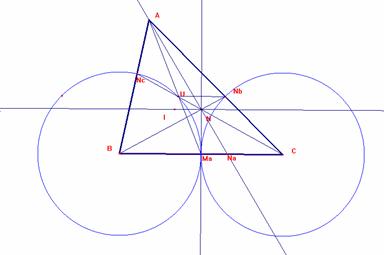
Siendo UN_bCB un trapecio isósceles, pues BU=CN_b la perpendicular media de las bases BC y N_bU pasará por N que es la intersección de las diagonales. Así la mediatriz de BC contiene a N.

b)      IG es paralela a BC y además IG = |AB - AC|/6.

Si trazamos I, es:

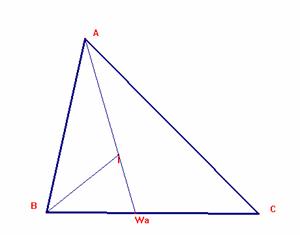
Es BW_a/AB=W_aC/AC. x/4c=(2b+2c-x)/4b.

4bx=8bc+8cc-4cx, x=(8bc+8cc)/(4b+4c)=2c.

Así, BW_a=2c, WaC=2b.

Luego es IA/IW_a= AB/BW_a=4c/2c=2. Así, AI/AW_a=2/3

Todo baricentro verifica que AG/AM_a = 2/3, donde Ma es el punto medio de BC.

Así, la recta IG es paralela a BC.

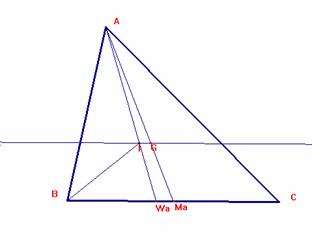
IG=2/3W_aM_a= 2/3(W_aC-M_aC)=2/3 (2b-(b+c))=2/3(b-c)=2/3((AB-AC)/4)=

(AB-AC)/6.

c)      IN es paralela a BC y además GN =|AB - AC|/3.

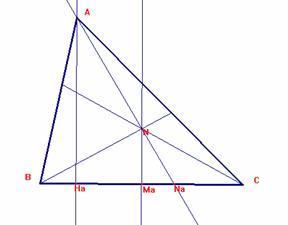
Tacemos la perpendicular a BC por N, es decir, la mediatriz de BC.

Es M_aC=b+c.

Sea N_a el punto en que la circunferencia exinscrita es tangente a BC.

Es N_aC=p-AC=3b+3c-4b=3c-b.

Luego M_aN_a =(c+b)-(3c-b)=2b-2c.

Sea AH_a la perpendicular a BC por A.

Sea BH_a=x, es H_aC=2b+2c-x.

AH_a²= (4c)²- x ²= (4b)² – (2b+2c-x)²

Es decir, 16c²-x²=16b² - (4b²+4c²+x²+8bc-4bx-4cx)

16c²=16b²  -4b² - 4c² - 8bc + 4bx + 4cx

16(c+b)(c-b)+ 4(b+c)(b+c)= 4x(b+c).

x= 4c-4b+b+c=5c-3b.

Así, H_aC = 2b+2c-(5c-3b)=5b-3c.

Por ello, H_aN_a=H_aC-N_aC= (5b-3c)-(3c-b)=6b-6c.

Luego al ser los triángulos AH_aNa y NM_aN_a semejantes, es

NN_a/AN_a = M_aN_a/H_aN_a = (2b-2c)/(6b-6c)=1/3.

Luego al ser GM_a/AM_a=1/3, G y N están sobre una paralela a M_aN_a, es decir a BC.

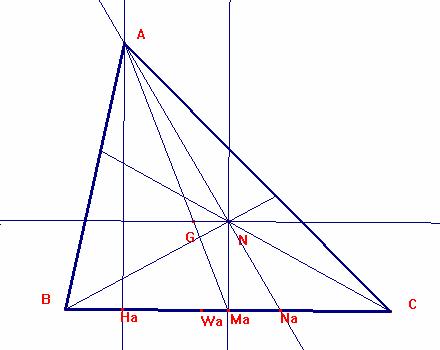
 GN=2/3(M_aN_a)=2/3(M_aC-N_aC)=2/3((b+c)-(3c-b))=2/3 (2b-2c)=(4b-4c)/3=(AC-AB)/3.

 

Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla