Solución de : Correa Pablo Ariel. Profesor de la ESB Nº42. Buenos Aires, Argentina.
|
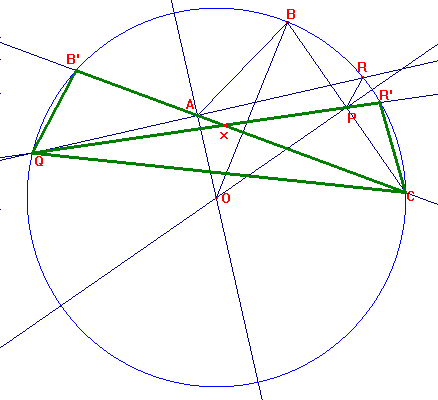
Propuesto por Ignacio Larrosa Cañestro, profesor del IES Rafae Dieste A Coruña Problema 371 Sean ABC un triángulo cualquiera no isósceles, P el punto medio del lado BC y Q ;R dos puntos sobre la bisectriz del ángulo A, simétricos respecto de A y tales que < QPC = < RPC. Entonces AB + AC = PQ + PR. mina_world (2006): sci.math
|

Descripción de las construcciones:
1.1) Determinamos la mediatriz del lado BC.
1.2) Construimos la recta perpendicular a la bisectriz del ángulo A por A.
1.3) Llamamos O al punto de intersección de las rectas anteriores. Creamos la C(O; OB) y denotamos por Q y R a los puntos de intersección de la circunferencia anterior con la bisectriz del ángulo A.
1.4) Trazamos la recta QP y señalamos con R’al punto de intersección de esta recta con la circunferencia.
1.5) Trazamos la recta AC y señalamos con B’al punto de intersección de esta recta con la circunferencia.
2) Algunas conclusiones:
2.1) Los segmentos RP y R’P son congruentes:
* <RPB = <BPQ por ser suplementarios de ángulos congruentes.
*<BPQ = <R’PC por ser opuestos por el vértice.
* 90º+<RPB
= 90º+<R’PC![]() <RPO = <R’PO.
<RPO = <R’PO.
* OP = OP por común.
* OR = OR’por ser radio de la circunferencia.
* Tenemos que los triángulos OPR y OPR’son congruentes por tener dos lados y el ángulo opuesto al mayor de ellos respectivamente congruentes. Entonces, RP =R’P por ser PCTCC.
2.2) Los segmentos BA y B’A son congruentes:
*< BAR =<RAC por propiedad de la bisectriz.
*<RAC =<B’AQ por ser opuestos por el vértice.
* 90º+< BAR = 90º+<B’AQ
![]() <BAO = <B’AO.
<BAO = <B’AO.
*AO =AO por común.
*OB = OB’por ser radio del la circunferencia.
* Tenemos que los triángulos OAB y OAB’son congruentes por tener dos lados y el ángulo opuesto al mayor de ellos respectivamente congruentes. Entonces, BA = B’A por ser PCTCC.
2.3) Hasta el momento tenemos que PQ + PR = PQ + PR’ y que AB + AC = AB’+AC.Faltaría demostrar que los triángulos R’CQ y B’CQ son congruentes.
3) Los segmentos BR y R’C son congruentes:
* BP = PC por ser P punto medio de AB.
*<RPB =<R’PC se demostró en el ítem 2.1
* RP =R’P se demostró en el ítem 2.1
*Los triángulos RPB y R’PC son congruentes. Entonces, BR =R’C por ser PCTCC.
4) Los segmentos BR y B’Q son congruentes:
*QA = AR por ser A punto medio del segmento QR.
*< BAR = <B’AQ se demostró en el ítem 2.2
* BA = B’A se demostró en el ítem 2.2
* Los triángulos BRA y B’QA son congruentes y se deduce que BR y B’Q también lo son.
5) Por el ítem3 tenemos que BR =R’C y por el 4, BR = B’Q.Entonces R’C = B’Q
6) <QR’C = <CB’Q por intersecar el mismo arco, QC.
7) <R’CB’=<R’QB’ por intersecar el mismo arco, B’R’.
8) Por lo desarrollado en 5,6 y 7 tenemos que el triángulo B’XQ es congruente con el triángulo R’XC por el postulado de la congruencia ALA. Por otra parte, se puede deducir el triángulo QXC es isósceles de ángulos congruentes: <XQC = <XCQ.
9)
<R’CB+<XCQ =<R’QB’+<XQC ![]() <R’CQ=<B’QC
<R’CQ=<B’QC
10) En
resumen: Hemos demostrado que: R’C = B’Q, <QR’C = <CB’Q y que <R’CQ=<B’QC.Por
lo tanto los triángulos R’CQ y B’CQ son congruentes por el postulado de la
congruencia ALA.
Siendo QR’=B’C
![]() PQ + PR’=AB’+AC
PQ + PR’=AB’+AC![]() PQ + PR = AB + AC. LQQD
PQ + PR = AB + AC. LQQD