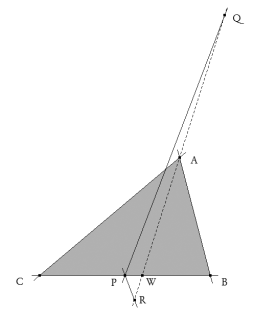
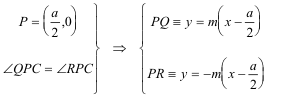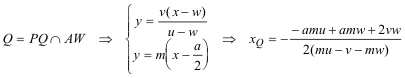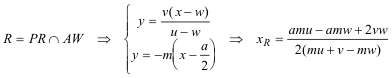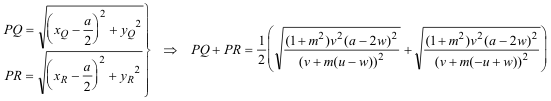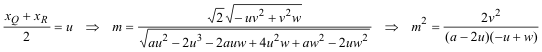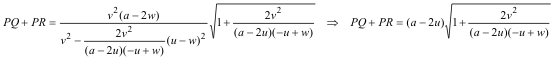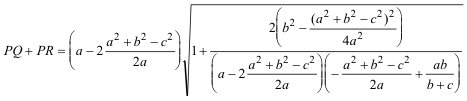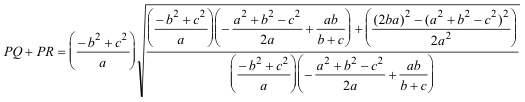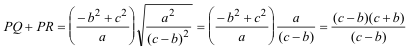De investigación . Propuesto por Ignacio Larrosa Cañestro, profesor del IES Rafael Dieste A Coruña Problema 371 Sean ABC un triángulo cualquiera no isósceles, P el punto medio del lado BC y Q;R dos puntos sobre la bisectriz del ángulo A, simétricos respecto de A y tales que <QPC = <RPC. Entonces AB + AC = PQ + PR. mina_world (2006): sci.math . Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (14 de enero de 2007) |
|
DISCUSIÓN |
|
En principio, después de estudiar el enunciado con CABRI II, no he sido capaz de obtener una solución fácil con él; es por ello que abordaré una solución POR FUERZA BRUTA utilizando algo de geometría analítica.
Para ello tomaremos un sistema de coordenadas cartesiano rectangular con origen en C y eje de abscisas CB. LAS COORDENADAS DE LOS VÉRTICES Como es habitual
Las coordenadas de A, B y C son
De las condiciones
nos queda
LA BISECTRIZ DEL ÁNGULO A La bisectriz del ángulo A es una recta que pasa por A y corta a CB en W. Por el teorema de la bisectriz podemos determinar W.
La ecuación de la bisectriz por A la determinaremos como la de la recta que pasa por A y W
LAS RECTAS PQ Y PR Son dos rectas que pasan por el punto P. La condición de que los ángulos <QPC y <RPC sean de la misma magnitud hace que las rectas tengan las pendientes iguales pero de signo contrario.
|
|
SOLUCIÓN |
|
DETERMINACIÓN DEL PUNTO Q
DETERMINACIÓN DEL PUNTO R
DETERMINACIÓN DE PQ+PR
que simplificando nos lleva a
IMPONEMOS LA CONDICIÓN QUE Q Y R SON SIMÉTRICOS RESPECTO DE A Con ello podemos determinar el valor de m, pendiente de PQ
Sustituimos m en PQ+PR y queda . . . . . . . .
IMPONEMOS LOS VALORES DE u, v, w
que nos llevan a
y ordenando
que simplificando queda como
de donde
|