De investigación.
Propuesto por Ignacio Larrosa Cañestro, profesor del
IES Rafael Dieste A Coruña
Problema 371.- Sean ABC un triángulo cualquiera no isósceles, P el punto medio del lado BC y Q;R dos
puntos sobre la bisectriz del ángulo A, simétricos respecto de A y tales que <QPC = <RPC. Entonces AB + AC = PQ + PR.
Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.-
La igualdad de los ángulos en P implica que el lado BC es la bisectriz del ángulo RPQ, por tanto podemos suponer que el punto P está sobre una elipse de focos R y Q pues para trazar la tangente a una elipse en un punto hay que hallar la bisectriz del ángulo formado por un radio vector y la prolongación del otro.
Su tangente es la mediatriz del lado BC.
Podemos suponer que el vértice A yace sobre otra elipse con focos B y C y centro P. Lo que hay que demostrar es que el eje principal de ambas es el mismo.
Es fácil hacer el dibujo de la elipse determinada por el triángulo. La bisectriz exterior de A es la tangente en A, la interior es la normal.
Para la otra podemos dibujarla suponiendo la veracidad del enunciado (hacemos trampa): sus ejes son las dos bisectrices de A y sería fácil de construir. Pero vamos a hacerlo sin presuponer nada.
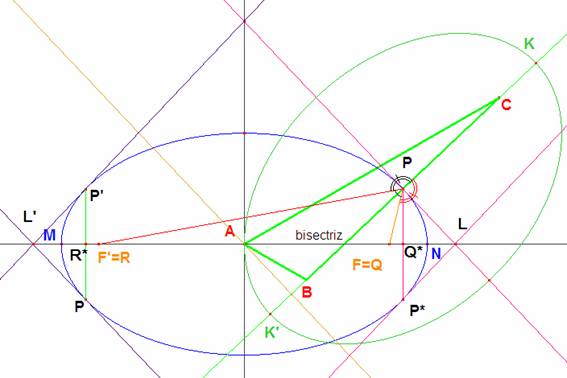
La elipse que buscamos pasa por P y por sus simétricos respecto de los ejes (rectas normal y tangente en A), los puntos P’, P” y P*. Nos falta un quinto punto para fijarla, pero tenemos la tangente en P. Por simetría, si PL es la tangente en P, P*L lo es en P*. La polar del punto L respecto de la elipse es la recta que une P y P*, por ello si llamamos M y N a los puntos de la elipse sobre el eje mayor (donde se encuentra L), la cuaterna formada por los puntos L, Q*, N y M es armónica.
Esta propiedad es la que vamos a usar para demostrar que las dos elipses tienen ejes principales de igual longitud. También sirve para construir los puntos M y N. Considerando los puntos simétricos L’ y R* que también están separados armónicamente por M y N tenemos sobre la bisectriz interior de A una involución en la que son homólogos (L, Q*) y (L’, R*). La involución queda definida conociendo un par de homólogos y sus puntos dobles (si los hay) son los puntos buscados.
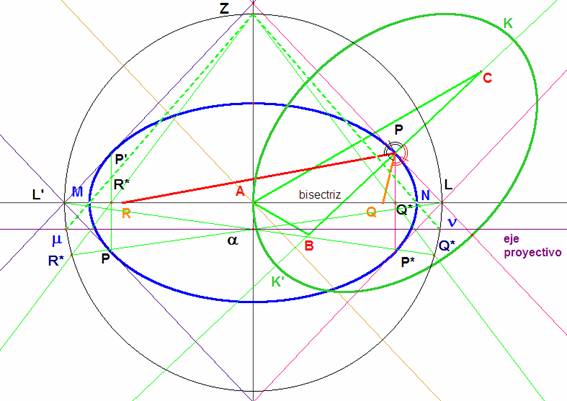
Para hallarlos proyectamos la involución sobre una circunferencia con centro el de la cónica y que pase por L (se puede proyectar sobre cualquier cónica, elegimos ésta por comodidad). El punto de proyección Z, puede ser uno de los puntos en que la circunferencia alcanza a la bisectriz exterior de A. Conservo el mismo nombre para los puntos proyectados. El eje de la involución proyectada corta a la circunferencia en los puntos dobles que, nuevamente proyectados sobre la bisectriz nos dan los puntos buscados.
La homografía sobre la circunferencia viene definida por (L, L’, Q*)à(Q*, R*, L).
El eje es la paralela a LL’ por a, construido según es habitual. Alcanza a la circunferencia en m y n.
Esta construcción sirve para tener perfectamente determinada la elipse, pero no nos proporciona la medida de su eje mayor.
Para efectuar
esta medida usaremos que la razón doble
de la cuaterna (L, Q*, N, M) es –1. En esta cuaterna si tomamos el
punto A como origen, los dos puntos últimos
son simétricos respecto a él. Si designamos las abscisas de L y
Q* por a y b, –x y x para M y N, tendremos para esa
razón doble 
que nos da,
resolviendo la ecuación 
. Así pues,
concluiremos el problema si logramos probar que el producto de las longitudes
de los segmentos AL y AQ* es a2 (donde llamamos a,
b y c a los parámetros de la
elipse que pasa por A y tiene focos
en B y C).
Este cálculo sirve también para construir los puntos N y M de forma más sencilla, aunque menos vistosa, como medias geométricas de los segmentos AL y AQ* para el primero y de AL’ y AR* para el segundo.
Para concluir, tomemos como ejes de coordenadas los de la elipse que pasa por A (lado BC y mediatriz).
Sea P(0,0)
y A(x0, y0) sobre la elipse 
, o bien b2x2 + a2y2 = b2a2.
(a y b son los semiejes y 2c la distancia focal).
La ecuación de la recta tangente en A es: b2x0x + a2y0y = b2a2, y la recta normal en ese
punto es a2y0x — b2x0y =
c2x0y0
La paralela a la tangente en A por P es: b2x0x + a2y0y = 0.
El punto L se obtiene cortando la normal con el
eje OY (x=0). L=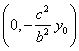
.
El vector AL=
, y llamando w = 
se puede poner AL=
. El módulo de w
es:
. (w es un vector de dirección de la normal
en A).
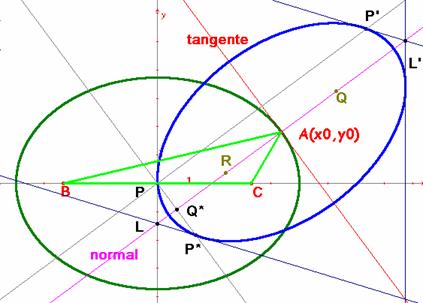
El punto Q* es el punto de intersección de la normal en A con la paralela a la tangente en A que pasa por P. Es la solución del sistema
b2x0x + a2y0y=0
a2y0x — b2x0y = c2x0y0
Resolviendo con cuidado, y también con paciencia, se obtiene
Q*=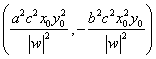
.
Para hallar el vector AQ* vamos a calcular cada coordenada paso a paso:
La x: Es una fracción con denominador 
y numerador un
producto de x0 por la
expresión
.
La y: También una fracción con denominador y numerador con un
factor y0 y otro igual a
.
Así pues
AQ*=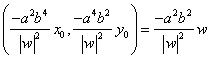
.
El producto de los módulos de los vectores AL y AQ* es igual al cuadrado del semieje mayor de esta elipse, ese valor resulta ser
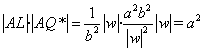
Por consiguiente las dos elipses tienen iguales los ejes mayores, como se pretendía demostrar.