Para el aula

Problema 372.

Relación entre las alturas de un triángulo y el inradio.

1/r = 1/h1 + 1/h2 + 1/h3

Campo, S. (2005) Métodos sintéticos de la geometría. Edición de autor. Salamanca. (p.9)

“El plan de estudios de Matemáticas en los institutos de enseñanza secundaria españoles apenas dedica unas pocas lecciones, repartidas en varios cursos, a la geometría…. La vieja geometría sintética, la de regla y compás, para el plano, está totalmente ausente en estos planes de estudios….” [Introducción]

Con permiso de su autor, a quien el director agradece su atención.

Referencia ofrecida por Ricard Peiró i Estruch, a quien el director agradece la atención.

GUSIEV, V. y otros(1989) Prácticas para resolver problemas matemáticos. Geometría. Editorial Mir. Moscou, Problema 299, pág. 65.

Solución del director.

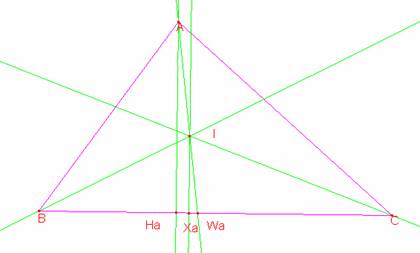
Sean H_a, X_a y W_a los pies de la altura, de la perpendicular desde el Incentro y de la bisectriz relativas al lado a.

Los triángulos AH_aW_a y IX_aW_a son semejantes

BW_a /W_aC=c/b

AI/IW_a=c/BW_a=b/W_aC=(c+b)/(BW_a+W_aC)=(c+b)/a.

Luego AW_a/IW_a =(c+b+a)/a.

Así, h_a/r=AH_a/IX_a= AW_a/IW_a =(c+b+a)/a.

r/h_a=a/(c+b+a).

De igual manera, r/h_b=b/(c+b+a), y r/h_c=c/(c+b+a).

Luego r/h_a +r/h_b+ r/h_c=(a+b+c)/(c+b+a)=1.

Así, 1/r= 1/h_a +1/h_b+ 1/h_c.

Ricardo Barroso Campos.

Didáctica de las Matemáticas.

Universidad de Sevilla