Para el aula

Problema 372.- Relación entre las alturas de un triángulo y el inradio. 

1/r = 1/h₁ + 1/h₂ + 1/h₃

Campo, S. (2005) Métodos sintéticos de la geometría. Edición de autor. Salamanca. (p.9)

“El plan de estudios de Matemáticas en los institutos de enseñanza secundaria españoles apenas dedica unas pocas lecciones, repartidas en varios cursos, a la geometría…. La vieja geometría sintética, la de regla y compás, para el plano, está totalmente ausente en estos planes de estudios….” [Introducción]

Con permiso de su autor, a quien el director agradece su atención.

Referencia ofrecida por Ricard Peiró i Estruch, a quien el director agradece la atención.

GUSIEV, V. y otros(1989) Prácticas para resolver problemas matemáticos. Geometría. Editorial Mir. Moscou, Problema 299, pág. 65.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

Si h es la altura sobre a de un triángulo y r el radio del círculo inscrito se tiene: 2·Área(ABC)= a·h = 2·pr, luego .

Haciendo esto para cada altura sobre a, b y c resulta

1=,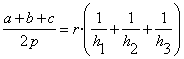

luego