De investigación

 Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

 Problema 373 

283.Demostrar que el perímetro de un triángulo acutángulo y el de su triángulo órtico son proporcionales a los radios de los círculos circuninscrito e inscrito en el primero.

 Matemática Elemental (1933) Tomo II, N.2, Febrero, pp. 26-29,

 Khayyam, O, (1964): American Mathematical Monthly, [E 1694](p.554). Resuelto entre otros por Bankoff, L.(1965, May, p.548)

 Altshiller-Court, N. (1925-1952): College Geometry, an introduction to the modern geometry of the triangle and the circle. Barnes & Noble. New York. (p. 100)

 Johnson, R.A. (1929-1960): Advanced Euclidean Geometry (formerly titled: Modern Geometry) An elementary treatise on the geometry of the triangle and the circle. Dover publications. Inc. New York. (p. 191)[Johnson señala que el problema lo estableció Karl Wilhem Feuerbach (1800-1834)

Solución tomada por el editor de Altshiller-Court, N. (1925-1952): College Geometry, an introduction to the modern geometry of the triangle and the circle. Barnes & Noble. New York. (p. 100)

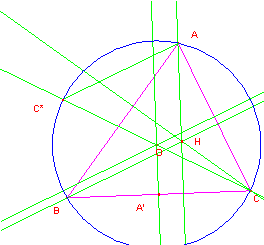
1.- Dado un triángulo ABC, y su órtico EFG, la distancia del circuncentro al lado a es la mitad de la distancia del vértice A al ortocentro H.

Hemos de ver que 2 OA’=AH. Trazamos el diámetro por C, CC*. BH es paralela a AC* pues ambas son perpendiculares a AC, BH por construcción de la altura y AC* por ser CC* diámetro. Por iguales razones, AH y C*B son paralelas, por lo que AHBC* es un paralelogramo y AH=C*B=2OA, por ser OA paralela media del triángulo rectángulo CBC*.

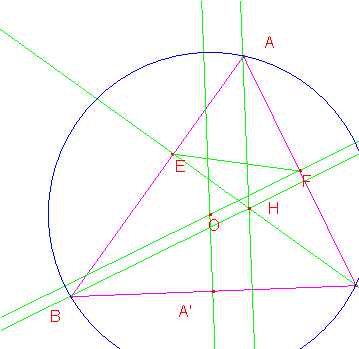
2.- BC/EF = R/Oa. La razón de un lado de un triángulo al correspondiente lado del órtico es igual a la razón del circunradio del original a la distancia del circuncentro al lado del original.

Al ser AH un diámetro de la circunferencia circunscrita a AEF, y ser AFE semejante a ABC, será BC/EF= 2R/AH=2R/2OA’=R/OA’.

Así, por 2, es: EF=(BC OA’)/R

De igual manera, FG=(BA OC’)/R, y EG=(AC OB’)/R.

Así, EF+FG+GE=(BC OA’+BA OC’+AC OB’)/R.

OA’ OB’ OC’ son las alturas de los triángulos OBC, OAC y OAB, por lo que es:

EF+FG+GE=(2[OBC]+2[OAC]+2[OAB])/R,

EF+FG+GE=(2[ABC])/R=((AB+BC+CA)r)/R.

Por último, cqd,

 (AB+BC+CA) /(EF+FG+GE) =R/r.

 

Por la transcripción,

Ricardo Barroso Campos.

Didáctica de las Matemáticas.

Universidad de Sevilla.