De investigación.

 Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.

Problema 373. 

283. Demostrar que el perímetro de un triángulo acutángulo y el de su triángulo órtico son proporcionales a los radios de los círculos circuninscrito e inscrito en el primero.

Matemática Elemental (1933) Tomo II, N.2, Febrero, pp. 26-29.

 Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca .-

Se tiene que AC’=b cos A, AB’=c cos A y por tanto AC’·AB=bc cos A=AB’·AC. Escrito De otro modo  que indica que los triángulos ABC y AB’C’ son semejantes. Con los triángulos formados en las otras esquinas  de ABC sucede lo mismo. Tenemos pues, cuatro triángulos semejantes al original compartiendo un vértice con él.

Sean p₀ el semiperímetro del triángulo órtico, R y r los radios de los círculos circunscrito e inscrito de ABC respectivamente.

La relación que se quiere probar   (1), equivale a

p · r=Área(ABC) = p₀ · R                 (2)

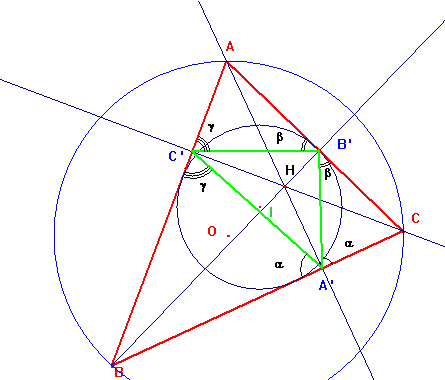
De la semejanza de ABC y AB’C’ deducimos fácilmente que el lado C’B’ mide a’= C’B’=a cos A  y como a=2R· sen A resulta finalmente a’= C’B’= R· sen 2A (también se podía obtener a partir del  ángulo del triángulo órtico en C’  que es 180- 2C y el radio de su circ. circunscrita –la de los nueve puntos- es R).

De este cálculo deducimos para el perímetro del triángulo órtico el valor

2p₀ =R(sen 2A + sen 2B+sen 2C)  (3)

Para el triángulo ABC se tiene, 2·Área(ABC)=absen C=4R² sen A· sen B ·sen C

Demostrar (1) ahora es equivalente a demostrar

4R² sen A· sen B ·sen C = R²(sen 2A + sen 2B + sen 2C)

o bien, simplificando

4sen A· sen B ·sen C = sen 2A + sen 2B + sen 2C     (4)

Al tratarse de un triángulo podemos expresar las razones del ángulo C por medio de las de A y B.  

sen C = sen(A+B) y  sen 2C = — sen (2A + 2B)

Sustituyendo en (4) resulta

4sen A· sen B · sen(A+B) = sen 2A + sen 2B — sen (2A + 2B)     (5).

Desarrollando sen(A+B) en el primer miembro y aplicando las fórmulas del ángulo doble se obtiene

2·sen 2B·sen² A+ 2·sen 2A·sen² B.

Aplicando la formula del seno de la suma de dos ángulos al segundo miembro de (5) obtenemos

 sen 2A(1-cos 2B) + sen 2B(1-cos 2A)= 2·sen 2A·sen² B+ 2·sen 2B·sen² A

después de usar las fórmulas del ángulo mitad. Y con esto se demuestra (5).

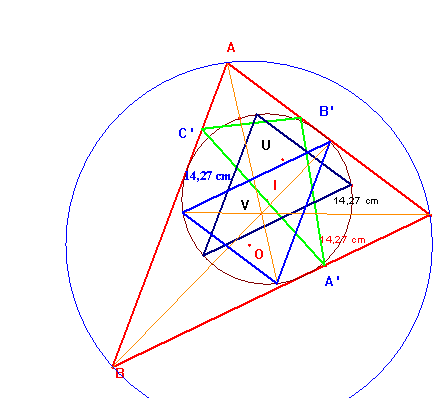
La relación demostrada nos dice que si aplicamos una homotecia que transforme la circunferencia circunscrita en la inscrita, el triángulo ABC se transforma en otro semejante a él que tiene igual perímetro que su triángulo órtico.

Hay dos homotecias de centros U y V respectivamente,  que transforman una circunferencia en la otra, por tanto habrá dos triángulos semejantes al primero con igual perímetro que el órtico.