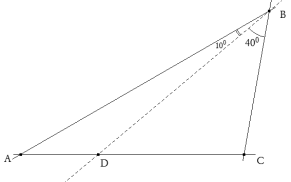
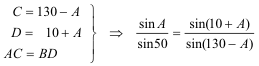De investigación

Problema 375

En el triángulo ABC se tiene D en AC tal que AC=BD y también <ABD=10º, <CBD=40º. Hallar <A.

Salazar, J. C. (2004): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (15 de febrero de 2007)

DISCUSIÓN

Para este enunciado propondremos dos procesos de solución

PRIMERA SOLUCION

Suponer el problema resuelto y utilizar el teorema de los senos y algo de trigonometría en los triángulos que se forman.

SEGUNDA SOLUCION

Construir el enunciado mediante la herramientas de CABRI II PLUS. Encontrar los distinto puntos D que cumplen con el enunciado (mediante lugares geométricos). Medir con CABRI los ángulos A así encontrados

.

PRIMERA SOLUCIÓN

Suponemos el problema resuelto

Aplicamos el teorema del seno al triángulo ABC

Aplicamos el teorema del seno al triángulo DBC

Como ángulos de un triángulo tenemos

De las dos primeras igualdades tenemos

Sustituyendo las igualdades de ángulos y la condición del enunciado

Ecuación que nos proporciona cuatro soluciones

Tomando como válidas las que hacen que D estén entre A y C, nos queda

SEGUNDA SOLUCIÓN

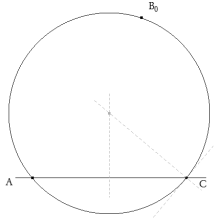
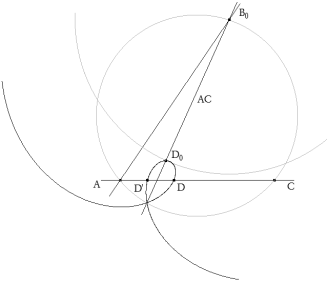
Como B es 50º, obtenemos el lugar de B como el arco capaz de 50º de la cuerda AC. Un punto cualquiera de ese lugar es B₀.

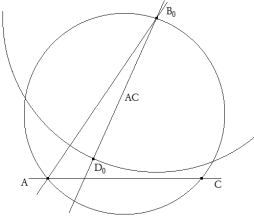
Trazamos un lado genérico AB₀, rotamos AB₀ 10º con centro en B₀ y con centro en B₀ y radio AC trazamos un arco que corta la recta rotada en D₀.

Si D₀ estuviera entre AC, ya tendríamos la solución; como, en general, no es así, hallamos el lugar geométrico de D₀ cuando B₀ recorre su arco capaz.

Este lugar corta a entre AC en los puntos D y D’.

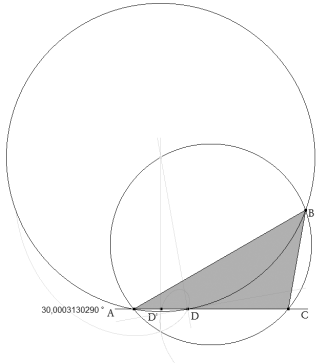
Para determinar B a partir de D, sabemos que el arco capaz de la cuerda AD es 10º. Trazamos dicho arco capaz que en su intersección con el lugar de los puntos B hallado al inicio nos proporciona B.

Usamos ahora CABRI II Plus para medir el ángulo A y nos da

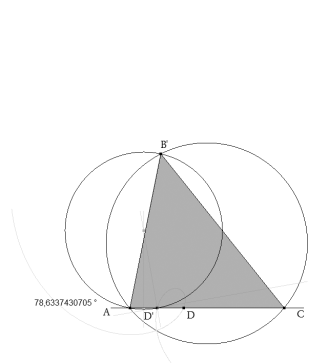
que como vemos presenta algo de ruido numérico.

Lo mismo haríamos a partir del punto D’ y obtendríamos B’ y el ángulo A’

De donde, tomando tres decimales