En un triangle . Siga D en el costat  tal que  i , . Determineu l’angle A.

Solució Ricard Peiró:

Siga .

A costat més gran li correspon l’angle oposat més gran.

, aleshores, .

, aleshores, .

Com que , aleshores, .

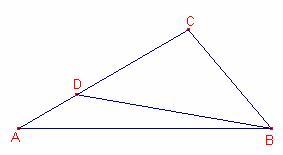Per tant, .

Aplicant el teorema dels sinus al triangle :

                          (1)

Aplicant el teorema dels sinus al triangle :

           (2)

Dividint les expressions (1) i (2):

                    (3)

Si resoles algebraicament l’equació amb DERIVE no ens dóna solució.

Considerem la funció:

La seua gràfica és:

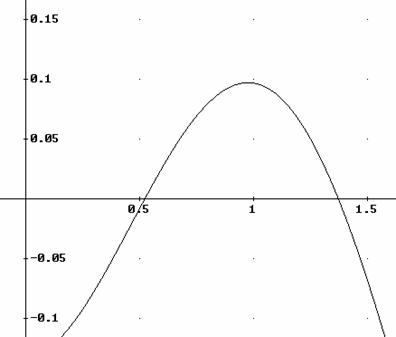
Calculem amb DERIVE les solucions aproximades de l’equació  

Les 2 solucions aproximades són:

Vegem que  és solució del problema:

Si , aleshores, , .

Aleshores el triangle  és isòsceles, .

Siga  l’altura del triangle .

. Aleshores, .

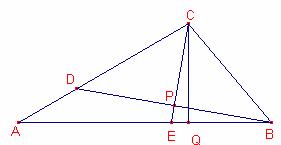Siga E el punt del costat  tal que .

La recta CE talla el segment  en el punt P.

Notem que .

 és altura del triangle isòsceles , aleshores, .

El triangle  és isòsceles, , , .

Aleshores els triangles rectangles ,  són iguals, aleshores:

.

Aleshores, .