En un triángulo . Sea D un punto en el lado  tal que  y , . Determinar el ángulo A.

Solución Ricard Peiró:

Sea .

Al lado más grande le corresponde ángulo opuesto más grande.

, entonces, .

, entonces, .

Como , entonces, .

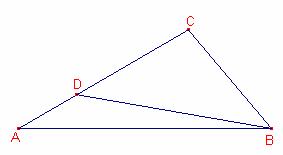Por tanto, .

Aplicando el teorema de los senos al triángulo :

                          (1)

Aplicando el teorema de los senos al triángulo :

           (2)

Dividiendo las expresiones (1) y (2):

                    (3)

Si resuelves algebraicamente la ecuación con DERIVE no nos da solución.

Consideremos la función:

La gráfica es:

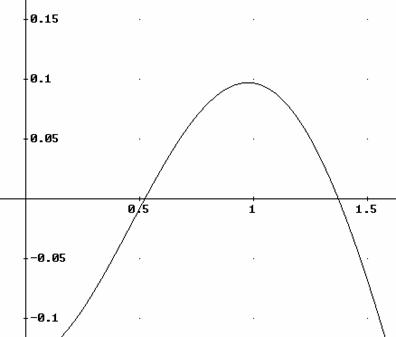
Calculemos con DERIVE las soluciones aproximadas de la ecuación  

Las 2 soluciones aproximadas son:

Veamos que  es solución del problema:

Si , entonces, , .

Entonces el triángulo  es isósceles, .

Sea  la altura del triángulo .

. Entonces, .

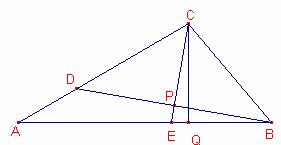Sea E el punto del lado  tal que .

La recta CE corta el segmento  en el punto P.

Notemos que .

 es altura del triángulo isósceles , entonces, .

El triángulo  es isósceles, , , .

Entonces los triángulos rectángulos ,  son iguales, entonces:

.

Entonces, .