Para el aula.

Problema 377. Dibújame por favor. Soy un triángulo rectángulo. Mi perímetro es de 10 cm. Mi altura desde el ángulo recto mide 2 cm. ¡Dibújame, por favor! Tu turno.

Berrondo-Agrell, M. (2006) 101 enigmas de geometría, juegos divertidos para potenciar tu mente. Ediciones Ceac Barcelona.(p.70). Ver en Librería Cervantes(4) , por ejemplo

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (11 de marzo de 2007)

DISCUSIÓN

Presentaremos la solución genérica para un triángulo rectángulo de altura h y perímetro 2p.

Supondremos el problema solucionado y veremos que con una propiedad de los puntos de contacto del círculo ex-inscrito opuesto al ángulo recto y con un lugar geométrico resolveremos el ejercicio.

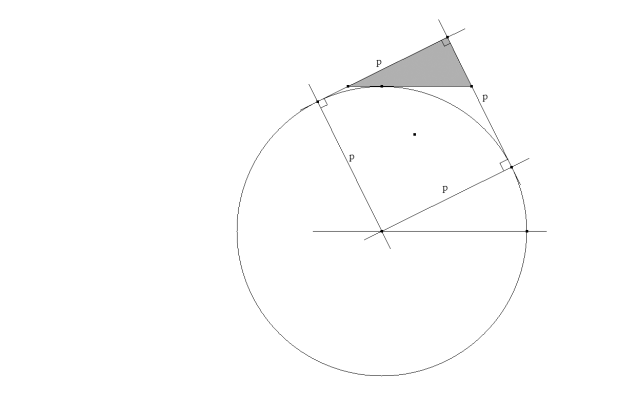
PRIMERO

La distancia desde el vértice a los puntos de contacto, sobre los lados en que se encuentra dicho vértice, del círculo ex-inscrito opuesto a dicho vértice es igual al semiperímetro p del triángulo.

En este caso, los ángulos rectos determinan un cuadrado que fija el radio ex-inscrito com p. La base del triángulo es tangente a este círculo.

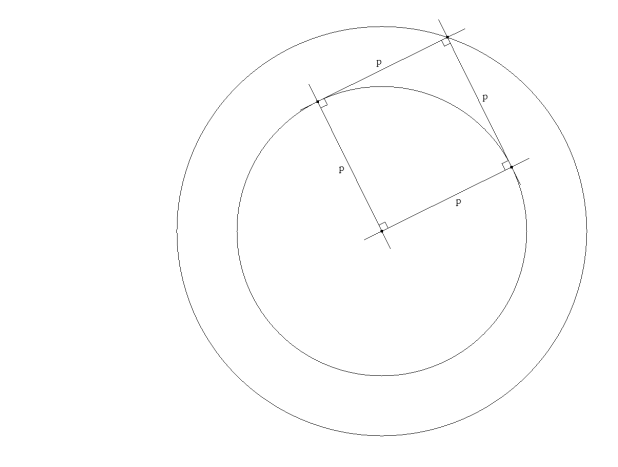
SEGUNDO

El lugar geométrico del punto de intersección de las tangentes a un círculo dado y que forman un ángulo fijo dado es un círculo concéntrico al anterior.

En nuestro caso, sobre este círculo está el vértice del ángulo recto.

SOLUCIÓN

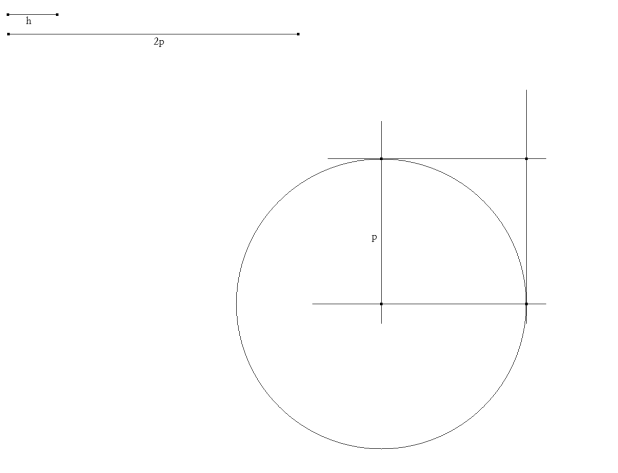
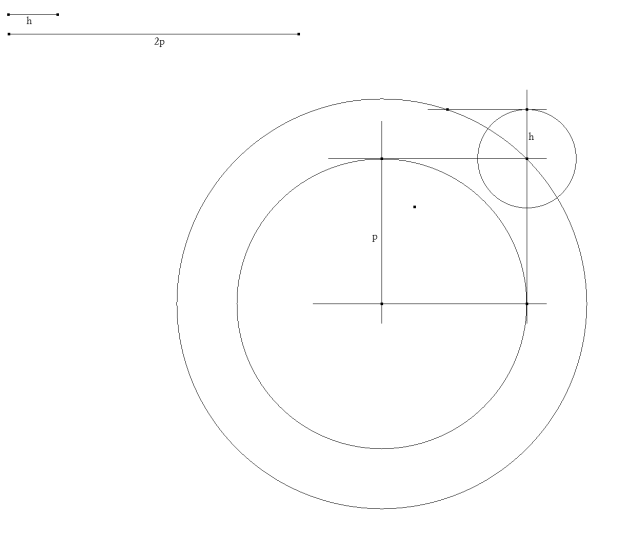
PRIMER PASO

Dado un segmento h y un segmento 2p, trazamos el círculo de radio p. Este círculo es el círculo ex-inscrito opuesto al vértice del ángulo recto del triángulo buscado.

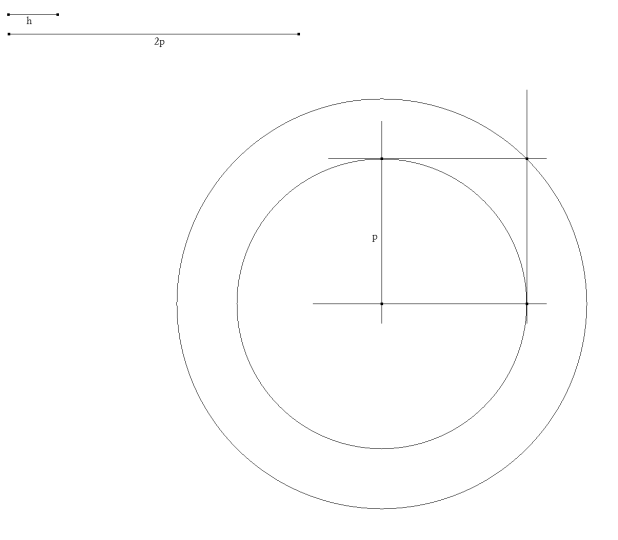
SEGUNDO PASO

Trazamos al círculo concéntrico al anterior que contiene el vértice del ángulo recto en el triángulo buscado.

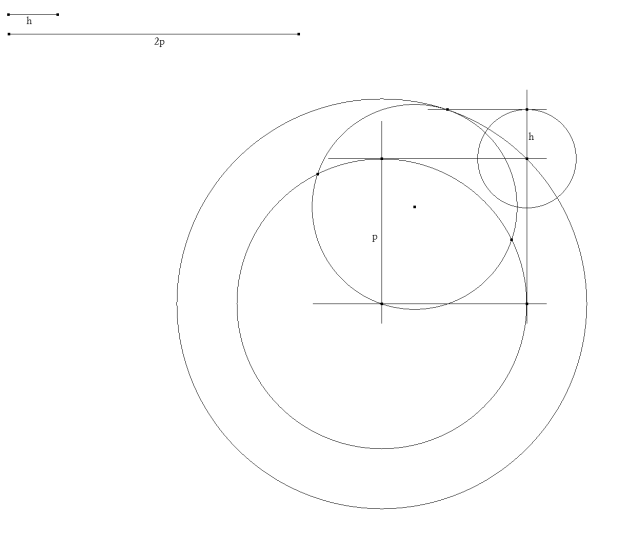
TERCER PASO

Sobre una tangente al círculo inicial, que contendrá a la base del triángulo, llevamos la altura h. Una paralela a distancia h de la base determina sobre el segundo círculo el vértice del ángulo recto del triángulo rectángulo buscado (Hay una segunda solución simétrica a la anterior).

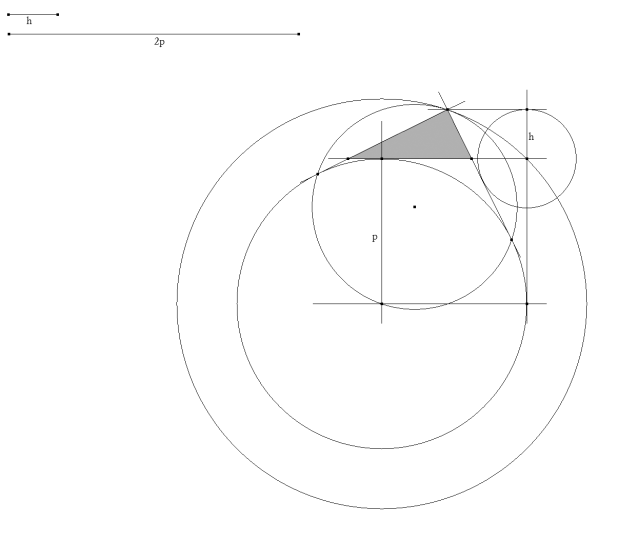
CUARTO PASO

Los catetos son las otras dos tangentes al círculo ex-inscrito que forman ángulo recto. Entonces desde el vértice del ángulo recto hallado determinamos los puntos de contacto con los catetos.

Para ello. Círculo que tiene por diámetro el vértice hallado y el centro del círculo ex-inscrito; su intersección con el círculo ex-inscrito nos determina el punto de contacto de cada cateto.

QUINTO PASO

Las rectas desde el vértice a los puntos de contacto hallados determinan los catetos que definen de manera unívoca el triángulo rectángulo buscado de altura h y perímetro 2p.

DISCUSIÓN

Si observamos las figuras trazadas, la altura nunca puede ser mayor que la diferencia de radios entre el círculo ex-inscrito opuesto al ángulo recto del triángulo y el círculo concéntrico al anterior que contiene al vértice del ángulo recto.

En el caso de la igualdad, la solución es única y el triángulo rectángulo es isósceles.